题目内容
(本小题满分10分)
如图14①至图14④中,两平行线AB、CD音的距离均为6,点M为AB上一定点.
思考:如图14①中,圆心为O的半圆形纸片在AB、CD之间(包括AB、CD),其直径MN在AB上,MN=8,点P为半圆上一点,设∠MOP=α,当α=________度时,点P到CD的距离最小,最小值为____________.
探究一在图14①的基础上,以点M为旋转中心,在AB、CD之间顺时针旋转该半圆形纸片,直到不能再转动为止.如图14②,得到最大旋转角∠BMO=_______度,此时点N到CD的距离是______________.
探究二将图14①中的扇形纸片NOP按下面对α的要求剪掉,使扇形纸片MOP绕点M在AB、CD之间顺时针旋转.
⑴如图14③,当α=60°时,求在旋转过程中,点P到CD的最小距离,并请指出旋转角∠BMO的最大值:
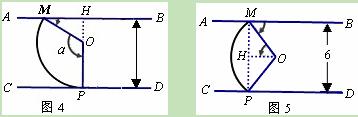
⑵如图14④,在扇形纸片MOP旋转过程中,要保证点P能落在直线CD上,请确定α的取值范围.
(参考数据:sin49°= ,cos41°=
,cos41°= ,tan37°=
,tan37°= )
)

解:思考 90,2.
探究一 30,2.
探究二、⑴由已知得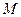 与
与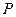 的距离为4,∴当
的距离为4,∴当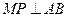 时,点
时,点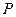 到
到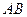 的最大距离是4,从而点
的最大距离是4,从而点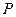 到
到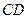 的最小距离为
的最小距离为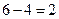 .
.
当扇形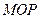 在
在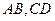 之间旋转到不能再转时,
之间旋转到不能再转时,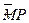 与
与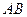 相切,此时旋转角最大,
相切,此时旋转角最大,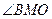 的最大值为90°.
的最大值为90°.
⑵如图4,由探究一可知,点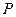 是
是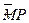 与
与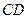 的切点时,
的切点时, 达到最大,即
达到最大,即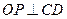 .此时,延长
.此时,延长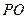 交
交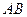 于点
于点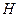 ,
, 最大值为
最大值为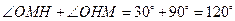 .
.
如图5,当点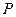 在
在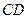 上且与
上且与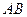 距离最小时,
距离最小时,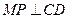 ,
, 达到最小,连接
达到最小,连接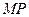 ,作
,作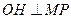 于点
于点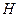 ,由垂径定理,得
,由垂径定理,得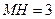 ,在
,在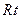 ⊿
⊿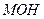 中,
中,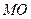 =4,
=4,
∴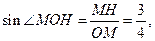 ∴
∴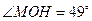 ,∵
,∵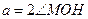 ,∴
,∴ 最小为
最小为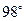 .
.
∴ 的取值范围是
的取值范围是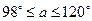 .
.
解析

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
 .
.



 的值.
的值.