题目内容
如图△ABC是等腰三角形，AB=AC，∠BAC=120°，点D在BC边上，且BD＜DC，以AD为边作
正三角形ADE，当△ABC的面积是25
，△ADE的面积是7
时，BD与DC的比值是（ ）
正三角形ADE，当△ABC的面积是25| 3 |
| 3 |
| A、3：4 | B、3：5 |
| C、1：2 | D、2：3 |
分析：根据△ABC的面积，可以计算AF，BF，设DF=x，根据△ADE的面积计算x的值，根据BD=BF-DF，CD=CF+DF即可计算BD，CD长度，即可计算BD：CD．
解答：解：作AF⊥BC，
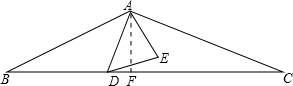
∵AB=AC，∠BAC=120°，∴∠ABC=30°，即AB=2AF．BF=
AF=
AF．
△ABC的面积为
×BC×AF=25
，计算得：AF=5，BF=5
．
设DF=x，则AD=
，
根据正三角形面积计算公式S=
AD×（
AD）=
AD2=7
，
计算得：x=
，
∴BD=BF-DF=4
，CD=CF+FD=6
，
故BD：CD=2；3，
故选 D．
∵AB=AC，∠BAC=120°，∴∠ABC=30°，即AB=2AF．BF=
| 22-1 |
| 3 |
△ABC的面积为
| 1 |
| 2 |
| 3 |
| 3 |
设DF=x，则AD=
| x2+52 |
根据正三角形面积计算公式S=
| 1 |
| 2 |
| ||
| 2 |
| ||
| 4 |
| 3 |
计算得：x=
| 3 |
∴BD=BF-DF=4
| 3 |
| 3 |
故BD：CD=2；3，
故选 D．
点评：本题考查了勾股定理的运用，考查了三角形面积的计算，本题中根据正三角形ADE计算DF是解题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
8、
1、如图，在△ABC中，D、E分别是AC、AB上的点，BD与CE交于点O，给出下列四个条件：①∠EBO=∠DCO；②∠BEO=∠CDO；③BE=CD；④OB=OC．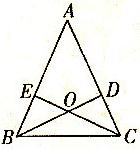
25、如图所示，在△ABC中，D、E分别是AC、AB上的点，BD与CE交于点0，给出下列三个条件：①∠EBO=∠DCO；②∠BEO=∠CDO；③BE=CD．
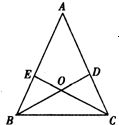17、如图，△ABC中，D、E分别是AC、AB上的点，BD与CE交于点O．给出下列三个条件：①∠EBO=∠DCO；②∠BEO=∠CDO；③BE=CD．上述三个条件中，哪两个条件可判定
如图，已知△ABC在平面直角坐标系中的位置如图，有以下五个结论：①点A的坐标是（0，3）；②把△ABC向左平移三个单位后，点B的对应点在函数
在△ABC中，∠ACB=90°，点A的坐标为（0，2），点B（-3，1）在抛物线y=ax2+ax-2上，点C在x轴上．