题目内容
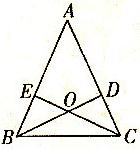 25、如图所示,在△ABC中,D、E分别是AC、AB上的点,BD与CE交于点0,给出下列三个条件:①∠EBO=∠DCO;②∠BEO=∠CDO;③BE=CD.
25、如图所示,在△ABC中,D、E分别是AC、AB上的点,BD与CE交于点0,给出下列三个条件:①∠EBO=∠DCO;②∠BEO=∠CDO;③BE=CD.(1)由上述三个条件中的①和③能判定△ABC是等腰三角形吗?请说明理由;
(2)除(1)中的一种情况外,还有哪两个条件可判定△ABC是等腰三角形(用序号写出所有情况),并证明.
分析:(1)能,根据已知利用AAS判定△BEO≌△CDO,根据全等三角形的对应边相等可得到OB=OC,再根据等边对等角可得到∠OBC=∠OCB,从而可推出∠ABC=∠ACB,即△ABC是等腰三角形.
(2)②③也可证明△ABC是等腰三角形,证法同(1).
(2)②③也可证明△ABC是等腰三角形,证法同(1).
解答:解:(1)能.
∵∠EBO=∠DCO,∠EOB=∠DOC,BE=CD,
∴△BEO≌△CDO,
∴OB=OC,
∴∠OBC=∠OCB,
∴∠ABC=∠ACB,
∴AB=AC,
∴△ABC是等腰三角形.
(2)②③.
∵∠BEO=∠CDO,∠EOB=∠DOC,BE=CD,
∴△BEO≌△CDO,
∴OB=OC,
∴∠OBC=∠OCB,
∴∠ABC=∠ACB,
∴AB=AC,
∴△ABC是等腰三角形.
∵∠EBO=∠DCO,∠EOB=∠DOC,BE=CD,
∴△BEO≌△CDO,
∴OB=OC,
∴∠OBC=∠OCB,
∴∠ABC=∠ACB,
∴AB=AC,
∴△ABC是等腰三角形.
(2)②③.
∵∠BEO=∠CDO,∠EOB=∠DOC,BE=CD,
∴△BEO≌△CDO,
∴OB=OC,
∴∠OBC=∠OCB,
∴∠ABC=∠ACB,
∴AB=AC,
∴△ABC是等腰三角形.
点评:此题主要考查等腰三角形的判定及全等三角形的判定与性质的综合运用.

练习册系列答案
 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
 如图所示,在△ABC中,∠A=47°,∠C=77°,DE∥BC,BF平分∠ABC,BF交DE于点F,求∠BFE的度数.
如图所示,在△ABC中,∠A=47°,∠C=77°,DE∥BC,BF平分∠ABC,BF交DE于点F,求∠BFE的度数.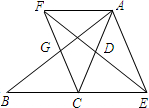 如图所示,在△ABC中,D是AC的中点,E是线段BC延长线上一点,过点A作AF∥BC交ED的延长线于点F,连接AE,CF.
如图所示,在△ABC中,D是AC的中点,E是线段BC延长线上一点,过点A作AF∥BC交ED的延长线于点F,连接AE,CF. 15、如图所示,在△ABC中,DM、EN分别垂直平分AB和AC,交BC于D、E,若∠DAE=50°,则∠BAC=
15、如图所示,在△ABC中,DM、EN分别垂直平分AB和AC,交BC于D、E,若∠DAE=50°,则∠BAC=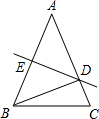 如图所示,在△ABC中,AB=AC,DE是边AB的垂直平分线,交AB于E,交AC于D,若△BCD的周长为18cm,△ABC的周长为30cm,那么BE的长为
如图所示,在△ABC中,AB=AC,DE是边AB的垂直平分线,交AB于E,交AC于D,若△BCD的周长为18cm,△ABC的周长为30cm,那么BE的长为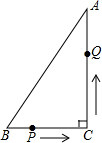 如图所示,在△ABC中,BC=7cm,AB=25cm,AC=24cm,P点在BC上从B点向C点运动(不包括点C),点P的运动速度为2cm∕s;Q点在AC上从C点向点A运动(不包括点A),运动速度为5cm∕s,若点P、Q分别从B、C同时运动,请解答下面的问题,并写出主要过程.
如图所示,在△ABC中,BC=7cm,AB=25cm,AC=24cm,P点在BC上从B点向C点运动(不包括点C),点P的运动速度为2cm∕s;Q点在AC上从C点向点A运动(不包括点A),运动速度为5cm∕s,若点P、Q分别从B、C同时运动,请解答下面的问题,并写出主要过程.