题目内容
 如图,已知△ABC在平面直角坐标系中的位置如图,有以下五个结论:①点A的坐标是(0,3);②把△ABC向左平移三个单位后,点B的对应点在函数y=-
如图,已知△ABC在平面直角坐标系中的位置如图,有以下五个结论:①点A的坐标是(0,3);②把△ABC向左平移三个单位后,点B的对应点在函数y=-| 8 | x |
分析:①根据平面直角坐标系写出点A的坐标即可判断;
②写出点B向左平移后的坐标,然后代入反比例函数解析式,符合则在图象上,否则不在;
③根据网格图形求出边AB、BC、AC的长度,然后再利用勾股定理逆定理进行判断;
④根据点B、C的坐标,利用待定系数法求出直线BC的解析式;
⑤根据△ABC是等腰直角三角形,利用三角形的面积公式计算即可.
②写出点B向左平移后的坐标,然后代入反比例函数解析式,符合则在图象上,否则不在;
③根据网格图形求出边AB、BC、AC的长度,然后再利用勾股定理逆定理进行判断;
④根据点B、C的坐标,利用待定系数法求出直线BC的解析式;
⑤根据△ABC是等腰直角三角形,利用三角形的面积公式计算即可.
解答:解:①点A的坐标是(3,0),故本小题错误;
②点B的坐标是(1,4),向左平移3个单位后是(-2,4),-
=4,
∴点B的对应点在函数y=-
的图象上,故本小题正确;
③根据勾股定理,AB=
=
,
BC=
=
,
AC=
=
,
∴AB=AC,且AB2+AC2=BC2,
∴△ABC是等腰直角三角形,故本小题正确;
④点B、C的坐标分别是(1,4),(-1,-2),
设直线BC的解析式是y=kx+b,
则
,
解得
,
∴边BC所在的直线解析式为y=3x+1,故本小题错误;
⑤△ABC的面积=
AB•AC=
×
×
=10,故本小题正确.
综上所述,正确的小题有②③⑤.
故答案为:②③⑤.
②点B的坐标是(1,4),向左平移3个单位后是(-2,4),-
| 8 |
| -2 |
∴点B的对应点在函数y=-
| 8 |
| x |
③根据勾股定理,AB=
| 22+42 |
| 20 |
BC=
| 22+62 |
| 40 |
AC=
| 22+42 |
| 20 |
∴AB=AC,且AB2+AC2=BC2,
∴△ABC是等腰直角三角形,故本小题正确;
④点B、C的坐标分别是(1,4),(-1,-2),
设直线BC的解析式是y=kx+b,
则
|
解得
|
∴边BC所在的直线解析式为y=3x+1,故本小题错误;
⑤△ABC的面积=
| 1 |
| 2 |
| 1 |
| 2 |
| 20 |
| 20 |
综上所述,正确的小题有②③⑤.
故答案为:②③⑤.
点评:本题考查了待定系数法求函数解析式,勾股定理,以及坐标的平移,都是基础知识,仔细分析图形,认真计算即可,难度不大.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,已知△ABC在直角坐标系中.
如图,已知△ABC在直角坐标系中. (2013•宜兴市一模)如图,已知△ABC在平面直角坐标系中,其中点A、B、C三点的坐标分别为(1,2
(2013•宜兴市一模)如图,已知△ABC在平面直角坐标系中,其中点A、B、C三点的坐标分别为(1,2 如图,已知△ABC在平面直角坐标系中的位置.
如图,已知△ABC在平面直角坐标系中的位置.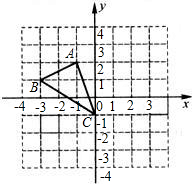 如图,已知△ABC在单位长度为1的网格中.
如图,已知△ABC在单位长度为1的网格中.