题目内容
△ABC是半径为
的圆内接三角形,以A为圆心,
为半径的⊙A与边BC相切于D点,则AB•AC的值为( )
| 15 |
| ||
| 2 |
A、
| ||||
| B、4 | ||||
C、
| ||||
D、3
|
分析:如图,点S是△ABC的外接圆圆心,作直径BE,连接EC,则∠BCE=90°;根据切线的性质可知AD⊥BC,由圆周角定理知∠A=∠E,sinA=sinE=BC:BE,利用S△ABC可求得AB•AC•
=AD•BC,代入对应数值即可求得AB•AC=3
.
| BC |
| BE |
| 10 |
解答: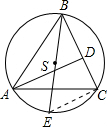 解:如图,点S是△ABC的外接圆圆心,作直径BE,连接EC,则
解:如图,点S是△ABC的外接圆圆心,作直径BE,连接EC,则
∠BCE=90°,BE=2
,
∵AD⊥BC
∴∠A=∠E,sinA=sinE=BC:BE,
∵S△ABC=
AB•AC•sinA=
AD•BC,
∴AB•AC•
=AD•BC,
∴AB•AC=3
.
故选D.
 解:如图,点S是△ABC的外接圆圆心,作直径BE,连接EC,则
解:如图,点S是△ABC的外接圆圆心,作直径BE,连接EC,则∠BCE=90°,BE=2
| 15 |
∵AD⊥BC
∴∠A=∠E,sinA=sinE=BC:BE,
∵S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
∴AB•AC•
| BC |
| BE |
∴AB•AC=3
| 10 |
故选D.
点评:本题利用了直径对的圆周角是直角,圆周角定理,三角形的面积公式求解.

练习册系列答案
相关题目
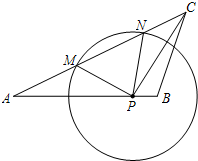 如图,已知在△ABC中,AB=15,AC=20,cotA=2,P是边AB上的一个动点,⊙P的半径为定长.当点P与点B重合时,⊙P恰好与边AC相切;当点P与点B不重合,且⊙P与边AC相交于点M和点N时,设AP=x,MN=y.
如图,已知在△ABC中,AB=15,AC=20,cotA=2,P是边AB上的一个动点,⊙P的半径为定长.当点P与点B重合时,⊙P恰好与边AC相切;当点P与点B不重合,且⊙P与边AC相交于点M和点N时,设AP=x,MN=y. 如图所示,弧AD是以等边三角形ABC一边AB为半径的四分之一圆周,P为弧AD上任意一点,若AC=5,则四边形ACBP周长的最大值是
如图所示,弧AD是以等边三角形ABC一边AB为半径的四分之一圆周,P为弧AD上任意一点,若AC=5,则四边形ACBP周长的最大值是