Question

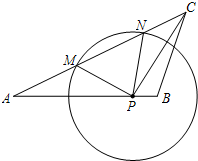如图，已知在△ABC中，AB=15，AC=20，cotA=2，P是边AB上的一个动点，⊙P的半径为定长．当点P与点B重合时，⊙P恰好与边AC相切；当点P与点B不重合，且⊙P与边AC相交于点M和点N时，设AP=x，MN=y．
（1）求⊙P的半径；
（2）求y关于x的函数解析式，并写出它的定义域；
（3）当AP=6

5

时，试比较∠CPN与∠A的大小，并说明理由．

Answer 1

分析：（1）作BD⊥AC，垂足为点D．则BD就是⊙P的半径．根据已知条件可求得sinA，即可得出BD，即⊙P的半径；
（2）作PH⊥MN，垂足为点H，由垂径定理，得MN=2MH．即可表示出PH，从而得出y关于x的函数解析式．
（3）当AP=6

5

时，可求出AM、CN．可证出△AMP∽△PNC，从而得出∠CPN与∠A的大小．

解答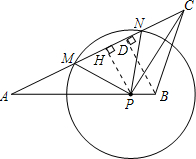：解：（1）作BD⊥AC，垂足为点D
∵⊙P与边AC相切，
∴BD就是⊙P的半径．
∵cotA=2，
∴sinA=

5

5

．（1分）
又∵sinA=

BD

AB

，AB=15，
∴BD=3

5

．（2分）

（2）作PH⊥MN，垂足为点H．
由垂径定理，得MN=2MH．（1分）
而PH=

5

5

x，PM=BD=3

5

，（1分）
∴y=2

45- 1 5 x2

，即y=

2

5

1125-5x2

．（2分）
定义域为3

5

≤x＜15．（1分）

（3）当AP=6

5

时，∠CPN=∠A．（1分）
证明如下：
当AP=6

5

时，PH=6，MH=3，AH=12，
∴AM=9．（1分）
∵AC=20，MN=6，
∴CN=5．（1分）
∵

AM

MP

=

9

3 5

=

3 5

5

，

PN

CN

=

3 5

5

，
∴

AM

MP

=

PN

CN

．（1分）
又∵PM=PN，
∴∠PMN=∠PNM．
∴∠AMP=∠PNC．（1分）
∴△AMP∽△PNC．（1分）
∴∠CPN=∠A．

点评：本题是一道中考压轴题，考查了切线的性质和垂径定理以及相似三角形的判定，难度偏大．