题目内容
(2014•静安区一模)已知点G是△ABC的重心,AB=AC=5,BC=8,那么AG=
2
2
.分析:根据题意画出图形,连接AG并延长交BC于点D,由等腰三角形的性质可得出AD⊥BC,再根据勾股定理求出AD的长,由三角形重心的性质即可得出AG的长.
解答: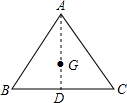 解:如图所示:连接AG并延长交BC于点D,
解:如图所示:连接AG并延长交BC于点D,
∵G是△ABC的重心,AB=AC=5,BC=8,
∴AD⊥BC,BD=
BC=
×8=4,
∴AD=
=
=3,
∴AG=
AD=
×3=2.
故答案为:2.
 解:如图所示:连接AG并延长交BC于点D,
解:如图所示:连接AG并延长交BC于点D,∵G是△ABC的重心,AB=AC=5,BC=8,
∴AD⊥BC,BD=
| 1 |
| 2 |
| 1 |
| 2 |
∴AD=
| AB2-BD2 |
| 52-42 |
∴AG=
| 2 |
| 3 |
| 2 |
| 3 |
故答案为:2.
点评:本题考查的是三角形的重心,熟知重心到顶点的距离与重心到对边中点的距离之比为2:1是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 (2014•静安区一模)如图,已知平行四边形ABCD中,向量
(2014•静安区一模)如图,已知平行四边形ABCD中,向量 (2014•静安区一模)如图,已知AB、CD分别表示两幢相距30米的大楼,小明在大楼底部点B处观察,当仰角增大到30度时,恰好能通过大楼CD的玻璃幕墙看到大楼AB的顶部点A的像,那么大楼AB的高度为( )
(2014•静安区一模)如图,已知AB、CD分别表示两幢相距30米的大楼,小明在大楼底部点B处观察,当仰角增大到30度时,恰好能通过大楼CD的玻璃幕墙看到大楼AB的顶部点A的像,那么大楼AB的高度为( )