Question

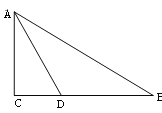
【题目】如图，在△ABC中，D为BC上一点，∠BAD=∠ABC，∠ADC=∠ACD，若∠BAC=63°，试求∠DAC、∠ADC的度数．

Answer 1

【答案】∠DAC=24°，∠ADC=78°

【解析】

试题分析：设∠BAD=x°，根据∠BAD=∠ABC得到∠ADC=2∠BAD，从而得到∠ACD=2∠BAD，根据三角形内角和定理列出方程求出x的值，从而得到答案.

试题解析：设∠BAD=．因为∠BAD=∠ABC，所以∠ADC=2∠BAD．又因为∠ADC=∠ACD，所以∠ACD=2∠BAD．因为∠BAC=63°，所以+∠DAC=63°，4+∠DAC=180°，所以∠DAC=24°，°，∠ADC=2×39°=78°．所以∠DAC=24°，∠ADC=78°．