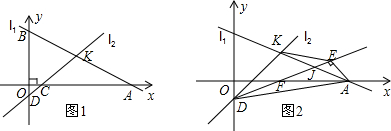题目内容
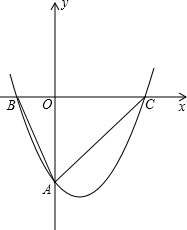
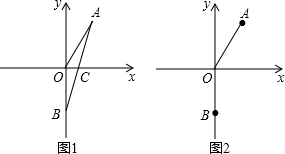
如图1,点A(a,6)在第一象限,点B(0,b)在y轴负半轴上,且a,b满足:(a-2
)2+|b+4|=0.
(1)求△AOB的面积.
(2)若线段AB与x轴相交于点C,在点C的右侧,x轴的上是否存在点D,使S△ACD=S△BOC?若存在,求出D点坐标;若不存在,请说明理由.
(3)如图2,若∠AOx轴=60°,射线OA绕O点以每秒4°的速度顺时针旋转到OA′,射线OB绕B点以每秒10°的速度顺时针旋转到O′B,当OB转动一周时两者都停止运动.若两射线同时开始运动,在旋转过程中,经过多长时间,OA′∥O′B?
| 3 |
(1)求△AOB的面积.
(2)若线段AB与x轴相交于点C,在点C的右侧,x轴的上是否存在点D,使S△ACD=S△BOC?若存在,求出D点坐标;若不存在,请说明理由.
(3)如图2,若∠AOx轴=60°,射线OA绕O点以每秒4°的速度顺时针旋转到OA′,射线OB绕B点以每秒10°的速度顺时针旋转到O′B,当OB转动一周时两者都停止运动.若两射线同时开始运动,在旋转过程中,经过多长时间,OA′∥O′B?

分析:(1)根据非负数的性质可得a-2
=0,b+4=0,再解方程即可;
(2)首先求出AB的直线解析式,再算出C点坐标,然后设D(a,0),根据S△ACD=S△BOC,可得
×6×(a-
)=4
,再解方程即可;
(3)此题要分两种情况进行讨论,①当∠1=∠2;②当∠3=∠4时分别计算.
| 3 |
(2)首先求出AB的直线解析式,再算出C点坐标,然后设D(a,0),根据S△ACD=S△BOC,可得
| 1 |
| 2 |
4
| ||
| 5 |
| 3 |
(3)此题要分两种情况进行讨论,①当∠1=∠2;②当∠3=∠4时分别计算.
解答: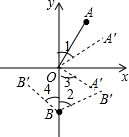 解:(1)∵(a-2
解:(1)∵(a-2
)2+|b+4|=0.
∴a-2
=0,b+4=0,
解得a=2
,b=-4;
∴A(2
,6),B(0.-4)
△AOB的面积为:
×4×2
=4
;
(2)设直线AB的关系式为y=mx+n,
∵A(2
,6),B(0.-4),
∴
,
解得
,
∴直线AB的关系式为y=
x-4,
当y=0时,x=
,
∴C(
,0),
设D(a,0),
∵S△ACD=S△BOC,
∴
×6×(a-
)=4
,
解得:a=
,
∴D点坐标(
,0);
(3)设x秒后OA′∥O′B,由题意得:
①当∠1=∠2时,(90-60)+4x=10x,
解得:x=5;
②当∠3=∠4时,180-(30+4x)=360-10x,
解得x=35,
答:在旋转过程中,经过10秒时间,OA′∥O′B.
 解:(1)∵(a-2
解:(1)∵(a-2| 3 |
∴a-2
| 3 |
解得a=2
| 3 |
∴A(2
| 3 |
△AOB的面积为:
| 1 |
| 2 |
| 3 |
| 3 |
(2)设直线AB的关系式为y=mx+n,
∵A(2
| 3 |
∴
|
解得
|
∴直线AB的关系式为y=
5
| ||
| 3 |
当y=0时,x=
4
| ||
| 5 |
∴C(
4
| ||
| 5 |
设D(a,0),
∵S△ACD=S△BOC,
∴
| 1 |
| 2 |
4
| ||
| 5 |
| 3 |
解得:a=
32
| ||
| 15 |
∴D点坐标(
32
| ||
| 15 |
(3)设x秒后OA′∥O′B,由题意得:
①当∠1=∠2时,(90-60)+4x=10x,
解得:x=5;
②当∠3=∠4时,180-(30+4x)=360-10x,
解得x=35,
答:在旋转过程中,经过10秒时间,OA′∥O′B.
点评:此题主要考查了平行线的判定与性质,一次函数解析式,以及非负数的性质,关键是考虑全面,不要漏解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

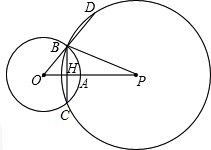 (2013•松江区模拟)已知:点A、B都在半径为9的圆O上,P是射线OA上一点,以PB为半径的圆P与圆O相交的另一个交点为C,直线OB与圆P相交的另一个交点为D,
(2013•松江区模拟)已知:点A、B都在半径为9的圆O上,P是射线OA上一点,以PB为半径的圆P与圆O相交的另一个交点为C,直线OB与圆P相交的另一个交点为D,