题目内容
(1)如图1,这是一个五角星ABCDE,你能计算出∠A+∠B+∠C+∠D+∠E的度数吗?为什么?(必须写推理过程)
(2)如图2,如果点B向右移动到AC上,那么还能求出∠A+∠DBE+∠C+∠D+∠E的大小吗?若能结果是多少?(可不写推理过程)
(3)如图,当点B向右移动到AC的另一侧时,上面的结论还成立吗?
(4)如图4,当点B、E移动到∠CAD的内部时,结论又如何?根据图3或图4,说明你计算的理由.

(2)如图2,如果点B向右移动到AC上,那么还能求出∠A+∠DBE+∠C+∠D+∠E的大小吗?若能结果是多少?(可不写推理过程)
(3)如图,当点B向右移动到AC的另一侧时,上面的结论还成立吗?
(4)如图4,当点B、E移动到∠CAD的内部时,结论又如何?根据图3或图4,说明你计算的理由.

分析:(1)根据三角形的一个外角等于与它不相邻的两个内角的和可得∠A+∠C=∠1,∠B+∠D=∠2,然后利用三角形的内角和定理列式即可得解;
(2)根据三角形的一个外角等于与它不相邻的两个内角的和可得∠A+∠D=∠1,在△BCE中,利用三角形的内角和列式计算即可得解;
(3)根据三角形的一个外角等于与它不相邻的两个内角的和可得∠A+∠C=∠1,∠B+∠D=∠2,然后利用三角形的内角和定理列式即可得解;
(4)延长CE与AD相交,根据三角形的一个外角等于与它不相邻的两个内角的和可得∠A+∠C=∠1,∠B+∠E=∠2,然后利用三角形的内角和定理列式即可得解.
(2)根据三角形的一个外角等于与它不相邻的两个内角的和可得∠A+∠D=∠1,在△BCE中,利用三角形的内角和列式计算即可得解;
(3)根据三角形的一个外角等于与它不相邻的两个内角的和可得∠A+∠C=∠1,∠B+∠D=∠2,然后利用三角形的内角和定理列式即可得解;
(4)延长CE与AD相交,根据三角形的一个外角等于与它不相邻的两个内角的和可得∠A+∠C=∠1,∠B+∠E=∠2,然后利用三角形的内角和定理列式即可得解.
解答: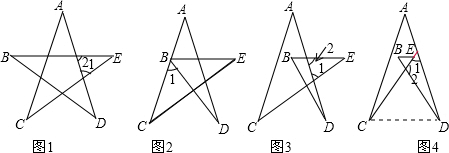 解:(1)如图,由三角形的外角性质,∠A+∠C=∠1,∠B+∠D=∠2,
解:(1)如图,由三角形的外角性质,∠A+∠C=∠1,∠B+∠D=∠2,
∵∠1+∠2+∠E=180°,
∴∠A+∠B+∠C+∠D+∠E=180°;
(2)如图,由三角形的外角性质,∠A+∠D=∠1,
∵∠1+∠DBE+∠C+∠E=180°,
∴∠A+∠DBE+∠C+∠D+∠E=180°;
(3)如图,由三角形的外角性质,∠A+∠C=∠1,∠B+∠D=∠2,
∵∠1+∠2+∠E=180°,
∴∠A+∠B+∠C+∠D+∠E=180°;
(4)如图,延长CE与AD相交,由三角形的外角性质,∠A+∠C=∠1,∠B+∠E=∠2,
∵∠1+∠2+∠D=180°,
∴∠A+∠B+∠C+∠D+∠E=180°.
 解:(1)如图,由三角形的外角性质,∠A+∠C=∠1,∠B+∠D=∠2,
解:(1)如图,由三角形的外角性质,∠A+∠C=∠1,∠B+∠D=∠2,∵∠1+∠2+∠E=180°,
∴∠A+∠B+∠C+∠D+∠E=180°;
(2)如图,由三角形的外角性质,∠A+∠D=∠1,
∵∠1+∠DBE+∠C+∠E=180°,
∴∠A+∠DBE+∠C+∠D+∠E=180°;
(3)如图,由三角形的外角性质,∠A+∠C=∠1,∠B+∠D=∠2,
∵∠1+∠2+∠E=180°,
∴∠A+∠B+∠C+∠D+∠E=180°;
(4)如图,延长CE与AD相交,由三角形的外角性质,∠A+∠C=∠1,∠B+∠E=∠2,
∵∠1+∠2+∠D=180°,
∴∠A+∠B+∠C+∠D+∠E=180°.
点评:本题考查了三角形的一个外角等于与它不相邻的两个内角的和的性质,三角形内角和定理,比较简单,关键在于准确识图,理清图中各角度之间的联系与转化.

练习册系列答案
相关题目
 6、如图所示的是一组数据的折线统计图,这组数据的极差是
6、如图所示的是一组数据的折线统计图,这组数据的极差是
 如图,点O是一段圆弧的圆心,AB是弦,AB=10cm,C是AB上一点,OC⊥AD于D,CD=1cm,求这段弧的半径.
如图,点O是一段圆弧的圆心,AB是弦,AB=10cm,C是AB上一点,OC⊥AD于D,CD=1cm,求这段弧的半径.