��Ŀ����
����Ŀ�������³�������ʱ��ɽ�ͽ��п��вι۵Ľ�ͨ���ߣ�С��һ��ȥij�����羰�����Σ����ȴ�ɽ��B��̨�ײ��е�A���ٻ����³���ɽ�D����B��A��·�߿ɿ������½�Ϊ50����б�£�����Ϊ3000�ף���A��D���³�·�߿ɿ���ֱ�ߣ���ˮƽ�ߵļн�Ϊ30�������³���A��D��ƽ���ٶ�Ϊ6m/s��ʱ��Ϊ10���ӣ���ɽ��D�ĸ߶ȣ����ο����ݣ�sin50���0.77��cos50���0.64��tan50���1.2��
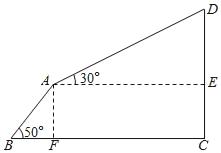
���𰸡�ɽ��D�ĸ߶�ԼΪ4110�ף�
��������
��A��AF��BC��F��AE��CD��E�����ı���AECF�Ǿ��Σ���ôCE=AF����ֱ�ǡ�ABF���AF����ֱ�ǡ�DAE���DE������CD=CE+DE����������𰸣�
��ͼ����A��AF��BC��F��AE��CD��E�����ı���AECF�Ǿ��Σ�
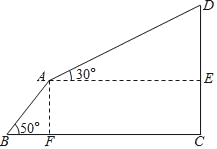
����ֱ����ABF�У���B=50�㣬
��AF=ABsin50���3000��0.77=2310��
��CE=AF��2310��
�����⣬�ɵ�AD=6��10��60=3600��
����ֱ����DAE�У���DAE=30�㣬
��DE=![]() AD=1800��
AD=1800��
��CD=CE+DE��2310+1800=4110���ף���
��ɽ��D�ĸ߶�ԼΪ4110�ף�

��ϰ��ϵ�д�
 ��������ܸ�ϰϵ�д�
��������ܸ�ϰϵ�д�
�����Ŀ