题目内容
四个三角形的边长分别为:①a=b=3
,c=6;②a=2,b=3,c=
;③a=2.5,b=6,c=6.5;④a=10.5,b=10,c=14.5.其中直角三角形的个数是( )
| 2 |
| 7 |
分析:求出a2+b2和c2的值,看看是否相等即可.
解答:解:∵a=b=3
,c=6,
∴a2+b2=(3
)2+(3
)2=36,c2=36,
∴a2+b2=c2,即三角形是直角三角形;
∵a=2,b=3,c=
,
∴a2+b2=22+32=13,c2=7,
∴a2+b2≠c2,即三角形不是直角三角形;
∵a=2.5,b=6,c=6.5,
a2+b2=2.52+62=42.25,c2=42.25,∵
∴a2+b2=c2,即三角形是直角三角形;
∵a=10.5,b=10,c=14.5
a2+b2=10.52+102=210.25,c2=210.25,
∴a2+b2=c2,即三角形是直角三角形;
即是直角三角形的有①③④,共3个,
故选B.
| 2 |
∴a2+b2=(3
| 2 |
| 2 |
∴a2+b2=c2,即三角形是直角三角形;
∵a=2,b=3,c=
| 7 |
∴a2+b2=22+32=13,c2=7,
∴a2+b2≠c2,即三角形不是直角三角形;
∵a=2.5,b=6,c=6.5,
a2+b2=2.52+62=42.25,c2=42.25,∵
∴a2+b2=c2,即三角形是直角三角形;
∵a=10.5,b=10,c=14.5
a2+b2=10.52+102=210.25,c2=210.25,
∴a2+b2=c2,即三角形是直角三角形;
即是直角三角形的有①③④,共3个,
故选B.
点评:本题考查了勾股定理的逆定理的应用,注意:如果一个三角形的两边a、b的平方和等于第三边c的平方,那么这个三角形是直角三角形.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目


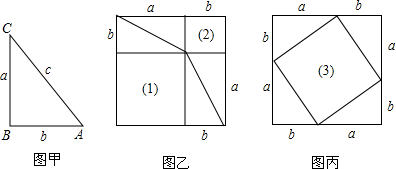
 ,c=6;②a=2,b=3,c=
,c=6;②a=2,b=3,c=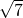 ;③a=2.5,b=6,c=6.5;④a=10.5,b=10,c=14.5.
;③a=2.5,b=6,c=6.5;④a=10.5,b=10,c=14.5.