Question

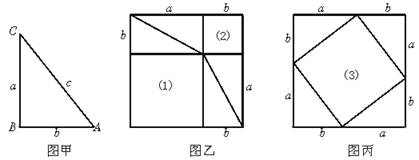
下图甲是任意一个直角三角形ABC，它的两条直角边的边长分别为a、b，斜边长为c．如图乙、丙那样分别取四个与直角三角形ABC全等的三角形，放在边长为a+b的正方形内．

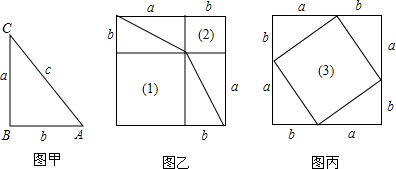
①图乙、图丙中（1）（2）（3）都是正方形．由图可知：（1）是以

a

为边长的正方形，（2）是以

b

为边长的正方形，（3）的四条边长都是

c

，且每个角都是直角，所以（3）是以

c

为边长的正方形．
②图中（1）的面积

a ²

，（2）的面积为

b ²

，（3）的面积为

c ²

．
③图中（1）（2）面积之和为

a²+b ²

．
④图中（1）（2）的面积之和与正方形（3）的面积有什么关系？为什么？由此你能得到关于直角三角形三边长的关系吗？

Answer 1

分析：根据图形可以直接得出各正方形的边长，进而得出各正方形面积，再通过两个组合正方形的面积之间相等的关系即可证明勾股定理．

解答：解：①图乙、图丙中（1）（2）（3）都是正方形．由图可知：（1）是以a为边长的正方形，（2）是以b为边长的正方形，
（3）的四条边长都是c，且每个角都是直角，所以（3）是以c为边长的正方形．
②图中（1）的面积a ²，（2）的面积为b ²，（3）的面积为c ²．
③图中（1）（2）面积之和为a²+b ²．
④由图乙和图丙可知大正方形的边长为：a+b，则面积为（a+b）²，
图乙中把大正方形的面积分为了四部分，分别是：边长为a的正方形，边长为b的正方形，还有两个长为b，宽为a的长方形，
根据面积相等得：（a+b）2=a2+b2+4×

1

2

ab，
由图丙可得（a+b）2=c2+4×

1

2

ab．
所以a²+b²=c²．
故答案为：①a，b，c，c；②a ²，b²，c ²；③a²+b ²．

点评：本题考查了利用图形面积的关系证明勾股定理，解题关键是利用三角形和正方形边长的关系进行组合图形，