题目内容
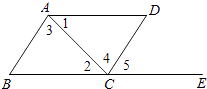
【题目】如图,两个全等的直角三角形重叠在一起,将其中的一个三角形沿着点B到C的方向平移到△DEF的位置,AB=10,DO=4,平移距离为6,则阴影部分面积为( ) 
A.24
B.40
C.42
D.48
【答案】D
【解析】解:∵△ABC沿着点B到C的方向平移到△DEF的位置,平移距离为6, ∴S△ABC=S△DEF , BE=6,DE=AB=10,
∴OE=DE﹣DO=6,
∵S阴影部分+S△OEC=S梯形ABEO+S△OEC ,
∴S阴影部分=S梯形ABEO= ![]() ×(6+10)×6=48.
×(6+10)×6=48.
故选D.
根据平移的性质得S△ABC=S△DEF , BE=6,DE=AB=10,则可计算出OE=DE﹣DO=6,再利用S阴影部分+S△OEC=S梯形ABEO+S△OEC得到S阴影部分=S梯形ABEO , 然后根据梯形的面积公式求解.

练习册系列答案
相关题目