Question

【题目】如图，已知抛物线C1交直线y=3于点A（﹣4，3），B（﹣1，3），交y轴于点C（0，6）．

（1）求C1的解析式．

（2）求抛物线C1关于直线y=3的对称抛物线的解析式；设C2交x轴于点D和点E（点D在点E的左边），求点D和点E的坐标．

（3）将抛物线C1水平向右平移得到抛物线C3，记平移后点B的对应点B′，若DB平分∠BDE，求抛物线C3的解析式．

（4）直接写出抛物线C1关于直线y=n（n 为常数）对称的抛物线的解析式．

Answer 1

【答案】（1）C1的解析式为y=x2+x+6；（2）抛物线C2的解析式为y=﹣x2﹣x，D（﹣5，0），E（0，0）；（3）抛物线C3的解析式为y=；（4）y=x2x+2n﹣6．

【解析】

（1）设抛物线C1经的解析式为y=ax2+bx+c，将点A、B、C的坐标代入求解即可得到解析式；

（2）先求出点C关于直线y=3的对称点的坐标为(0,0)，设抛物线C2的解析式为y=a1x2+b1x+c1，即可求出答案；

（3）如图，根据平行线的性质及角平分线的性质得到BB′=DB，利用勾股定理求出DB的长度即可得到抛物线平移的距离，由此得到平移后的解析式；

（4）设抛物线C1关于直线y=n（n 为常数）对称的抛物线的解析式为y=mx+nx+k，根据对称性得到m、n的值，再利用对称性得到新函数与y轴交点坐标得到k的值，由此得到函数解析式.

（1）设抛物线C1经的解析式为y=ax2+bx+c，

∵抛物线C1经过点A（﹣4，3），B（﹣1，3），C（0，6）．

∴,

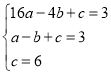解得，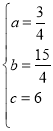

∴C1的解析式为y=x2+x+6；

（2）∵C点关于直线y=3的对称点为（0，0），

设抛物线C2的解析式为y=a1x2+b1x+c1，

∴，

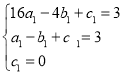解得，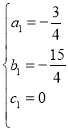

∴抛物线C2的解析式为y=﹣x2﹣x；

令y=0，则﹣x2﹣x=0，

解得x1=0，x2=﹣5，

∴D（﹣5，0），E（0，0）；

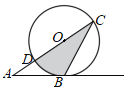
（3）如图，

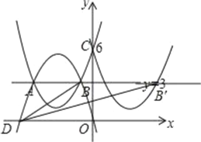
∵DB′平分∠BDE，

∴∠BDB′=∠ODB′，

∵AB∥x轴，

∴∠BB′D=∠ODB′，

∴∠BDB′=∠BB′D，

∴BB′=DB，

∵BD==5，

∴将抛物线C1水平向右平移5个单位得到抛物线C3，

∵C1的解析式为y=x2+x+6=（x+）2+，

∴抛物线C3的解析式为y=（x+﹣5）2+=；

（4）设抛物线C1关于直线y=n（n 为常数）对称的抛物线的解析式为y=mx+nx+k，

根据对称性得：新抛物线的开口方向与原抛物线的开口方向相反，开口大小相同，故m=-，对称轴没有变化，故n=-，

当n>6时，n+（n-6）=2n-6，故新抛物线与y轴的交点为（0，2n-6），

当n<6时，n-（6-n）=2n-6，新抛物线与y轴的交点为（0，2n-6），

∴k=2n-6，

∴抛物线C1关于直线y=n（n 为常数）对称的抛物线的解析式为：y=﹣x2﹣x+2n﹣6.