题目内容
【题目】如图,点F是CD 的中点,且AF⊥CD,BC=ED,∠BCD=∠EDC.
(1)求证:BF=EF;
(2)求证:AB=AE.

【答案】(1)、证明过程见解析;(2)、证明过程见解析
【解析】
试题分析:(1)、根据中点定义可得CF=DF,然后证明△BCF≌△EDF,进而可得FB=FE;(2)、根据△BCF≌△EDF可得FB=EF,∠BFC=∠EFD,再证明∠BFA=∠EFA,然后判定△ABF≌△AEF可得AB=AE.
试题解析:(1)、∵点F是CD 的中点, ∴CF=DF,
在△BCF和△EDF中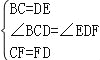 , ∴△BCF≌△EDF(SAS), ∴FB=FE;
, ∴△BCF≌△EDF(SAS), ∴FB=FE;
(2)、∵△BCF≌△EDF, ∴FB=EF,∠BFC=∠EFD, ∵AF⊥CD, ∴∠BFC+∠AFB=∠AFE+∠EFD,
∴∠BFA=∠EFA, 在△ABF和△AEF中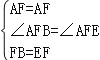 , ∴△ABF≌△AEF(SAS), ∴AB=AE.
, ∴△ABF≌△AEF(SAS), ∴AB=AE.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目