题目内容
【题目】计算：
（1）﹣82+72÷36
（2）2 
× 
÷（﹣9+19）
（3）（ ﹣ 
+ 
）×（﹣36）
（4）1 × 
﹣（﹣ ）×2 +（﹣ ）÷1 
（5）﹣13﹣（1﹣0.5）× 
×[2﹣（﹣3）2]．
【答案】
（1）解：﹣82+72÷36=﹣82+2
=﹣80
（2）解：2 
× 
÷（﹣9+19）= 
× × 
= 
（3）解：（ ﹣ 
+ 
）×（﹣36）=﹣18+20﹣21
=﹣19
（4）解：1 × 
﹣（﹣ ）×2 +（﹣ ）÷1 
= ×（ + ﹣ ）
= × 
= 
（5）解：﹣13﹣（1﹣0.5）× 
×[2﹣（﹣3）2]=﹣1﹣ × ×（﹣7）
=﹣1+ 
= 
【解析】（1）先算除法，再算加法即可；（2）先算括号里面的，再从左到右依次计算即可；（3）根据乘法的分配律进行计算即可；（4）根据乘法的分配律的逆运算进行计算即可；（5）先算乘方，再算乘除，最后算加减即可．
【考点精析】本题主要考查了有理数的四则混合运算的相关知识点，需要掌握在没有括号的不同级运算中，先算乘方再算乘除，最后算加减才能正确解答此题．
【题目】如果一个多边形的各边都相等，且各内角也都相等，那么这个多边形就叫做正多边形．如图，就是一组正多边形，观察每个正多边形中∠α的变化情况： 
（1）将下面的表格补充完整：
（2）根据规律，是否存在一个正多边形，其中的∠α=21°？若存在，请求出n的值，若不存在，请说明理由．
正多边形边数 | 3 | 4 | 5 | 6 | … | n |
∠α的度数 | 60° | … |
【题目】问题情景：
如图，在直角坐标系xOy中,点A、B为二次函数y=ax2(a>0)图象上的两点，且点A、B的横坐标分别为m、n(m>n>0),连接OA、AB、OB.设△AOB的面积为S时，解答下列问题:
探究：当a=1时，
mn | m | S | |
m=3,n=1 | 3 | 2 | |
m=5,n=2 | 10 | 3 |
当a=2时，
2mn | m | S | |
m=3,n=1 | 6 | 2 | |
m=5,n=2 | 20 | 3 |
归纳证明：
对任意m、n(m>n>0),猜想S=_________________ (用a,m,n表示)，并证明你的猜想.
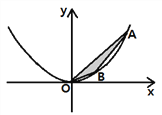
拓展应用：
若点A、B的横坐标分别为m、n(m>0>n),其它条件不变时，△AOB的面积S=____ (用a, m,n表示).
