题目内容
【题目】如图,在△ABC中,AB=1,AC=2,现将△ABC绕点C顺时针旋转90°得到△A′B′C′ , 连接AB′,并有AB′=3,则∠A′的度数为( )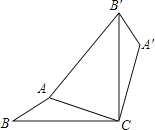
A.125°
B.130°
C.135°
D.140°
【答案】C
【解析】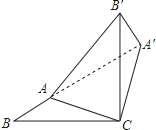
如图,连接AA′.由题意得:
AC=A′C , A′B′=AB , ∠ACA′=90°,
∴∠AA′C=45°,AA′2=22+22=8;
∵AB′2=32=9,A′B′2=12=1,
∴AB′2=AA′2+A′B′2 ,
∴∠AA′B′=90°,∠A′=135°,
故选C.
如图,作辅助线;首先证明∠AA′C=45°,然后证明AB′2=AA′2+A′B′2 , 得到∠AA′B′=90°,进而得到∠A′=135°,即可解决问题.

练习册系列答案
相关题目