题目内容
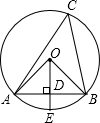 如图,AB是⊙O的弦,OD⊥AB于D交⊙O于E,则下列说法中:①AD=BD;②∠ACB=∠AOE;③AE=BE;④OD=DE,其中正确的序号有
如图,AB是⊙O的弦,OD⊥AB于D交⊙O于E,则下列说法中:①AD=BD;②∠ACB=∠AOE;③AE=BE;④OD=DE,其中正确的序号有分析:由AB为圆的直径,且与OD垂直,根据垂径定理得到D为AB中点,且E为弧AB的中点,即弧AE等于弧BE,由D为AB中点得到AD=BD,故选项①正确;由等弧对等弦得到AE=BE,故选项③正确;再由等弧对等角得到∠AOE=∠BOE=
∠AOB,又根据同弧所对的圆周角等于它所对圆心角的一半,得到∠ACB=
∠AOB,等量代换即可得到∠ACB=∠AOE,故选项②正确;若OD=DE,即可得到OD等于半径OA的一半,根据直角三角形中一直角边等于斜边的一半,这条直角边所对的角为30°,而原题没有此条件,故选项④错误.
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:∵AB是⊙O的弦,OD⊥AB于D交⊙O于E,
∴D为AB的中点,且
=
,
∴AD=BD,选项①正确;
∴AE=BE(等弧对等弦),选项③正确;
∵
=
,
∴∠AOE=∠BOE=
∠AOB,
又∵圆心角∠AOB和圆周角∠ACB都对
,
∴∠ACB=
∠AOB,
∴∠AOE=∠ACB,选项②正确;
若OD=DE,得到OD=
OE=
OA,又△ADO为直角三角形,
∴∠OAD=30°,题中没有此条件,选项④错误,
综上,正确的选项有①②③.
故答案为:①②③
∴D为AB的中点,且
 |
| AE |
 |
| BE |
∴AD=BD,选项①正确;
∴AE=BE(等弧对等弦),选项③正确;
∵
 |
| AE |
 |
| BE |
∴∠AOE=∠BOE=
| 1 |
| 2 |
又∵圆心角∠AOB和圆周角∠ACB都对
 |
| AB |
∴∠ACB=
| 1 |
| 2 |
∴∠AOE=∠ACB,选项②正确;
若OD=DE,得到OD=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠OAD=30°,题中没有此条件,选项④错误,
综上,正确的选项有①②③.
故答案为:①②③
点评:此题考查了垂径定理,以及圆周角定理,垂径定理可理解为:如果一条直线满足:过圆心、平分弦、垂直弦、平分优弧、平分劣弧这五个结论中的任两个,其余三个结论一定成立,对圆周角和圆心角进行相互转换是处理圆周角、圆心角问题时常用的方法,同时注意同圆或等圆中,弧、弦及圆心角,若一组对应量相等,其余两对对应量也相等.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
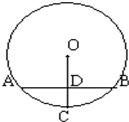 5、已知:如图,AB是⊙O的弦,半径OC⊥AB于点D,且AB=8m,OC=5m,则DC的长为( )
5、已知:如图,AB是⊙O的弦,半径OC⊥AB于点D,且AB=8m,OC=5m,则DC的长为( )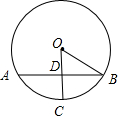 如图,AB是⊙O的弦,⊙O半径为5,OC⊥AB于D,交⊙O于C,且CD=2,则AB=
如图,AB是⊙O的弦,⊙O半径为5,OC⊥AB于D,交⊙O于C,且CD=2,则AB=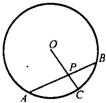 14、已知:如图,AB是⊙O的弦,半径OC交弦AB于点P,且AB=10cm,PB=4cm,PC=2cm,则OC的长等于
14、已知:如图,AB是⊙O的弦,半径OC交弦AB于点P,且AB=10cm,PB=4cm,PC=2cm,则OC的长等于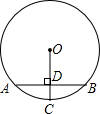 如图,AB是⊙O的弦,AB=10,⊙O的半径OC⊥AB于D,如果OD:DC=3:2,那么⊙O的直径长为
如图,AB是⊙O的弦,AB=10,⊙O的半径OC⊥AB于D,如果OD:DC=3:2,那么⊙O的直径长为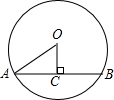 如图,AB是⊙O的弦,OC⊥AB于点C,若AB=4,OC=1,则⊙O的半径为( )
如图,AB是⊙O的弦,OC⊥AB于点C,若AB=4,OC=1,则⊙O的半径为( )