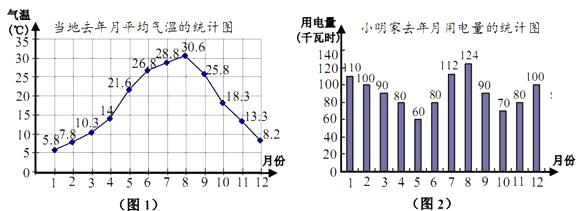
题目内容
【题目】已知一个正三角形和一个正六边形的周长相等，求它们的面积的比值．
【答案】解：设它们的周长是1．根据题意，得
正三角形的边长是 
，正六边形的边长是 
则正三角形的边心距是 
，正六边形的边心距是 
则正三角形的面积是 
，正六边形的面积是 
则它们的面积比是2：3．
【解析】根据正多边形的面积等于周长与边心距的乘积的一半，所以只需根据它们的周长计算其边心距；在由正多边形的半径、边心距和边长组成的直角三角形中，根据锐角三角函数的概念可以分别求得它们的边心距，再进一步计算其面积，从而得到其比值．
【考点精析】通过灵活运用正多边形和圆，掌握圆的内接四边形的对角互补，并且任何一个外角都等于它的内对角；圆的外切四边形的两组对边的和相等即可以解答此题．
练习册系列答案
阅读快车系列答案
相关题目
