题目内容
【题目】如图，抛物线y=ax2+bx+c（a≠0）过点（﹣1，0）和点（0，﹣3），且顶点在第四象限，设P=a+b+c，则P的取值范围是（ ）
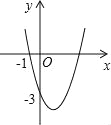
A. ﹣3＜P＜﹣1 B. ﹣6＜P＜0 C. ﹣3＜P＜0 D. ﹣6＜P＜﹣3
【答案】B
【解析】利用二次函数图象的开口方向和对称轴求出a＞0，b＜0，把x=﹣1代入求出b=a﹣3，把x=1代入得出P=a+b+c=2a﹣6，求出2a﹣6的范围即可．
解：∵抛物线y=ax2+bx+c（c≠0）过点（﹣1，0）和点（0，﹣3），
∴0=a﹣b+c，﹣3=c，
∴b=a﹣3，
∵当x=1时，y=ax2+bx+c=a+b+c，
∴P=a+b+c=a+a﹣3﹣3=2a﹣6，
∵顶点在第四象限，a＞0，
∴b=a﹣3＜0，
∴a＜3，
∴0＜a＜3，
∴﹣6＜2a﹣6＜0，
即﹣6＜P＜0．
故选：B．
“点睛”此题主要考查了二次函数图象的性质，根据图象过（﹣1，0）和点（0，﹣3）得出a与b的关系，以及当x=1时a+b+c=P是解决问题的关键．
练习册系列答案
相关题目
