题目内容
【题目】如图,一艘潜艇在海面下500米深处的A点,测得正前方俯角为31.0°方向上的海底有黑匣子发出的信号,潜艇在同一深度保持直线航行500米,在B点处测得海底黑匣子位于正前方俯角为36.9°的方向上,求海底黑匣子C所在点距离海面的深度.(精确到1米)(参考数据:sin36.9° ≈ 0.60,cos36.9° ≈ 0.80,tan36.9° ≈0.75,sin31.0°≈ 0.51,cos31.0°≈0.87 ,tan31.0°≈ 0.60)
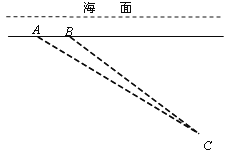
【答案】海底黑匣子C所在点距离海面的深度为2000米.
【解析】
试题分析:首先作CD⊥AB于D,依题意,AB=500米,∠DAC=31.0°,∠CBD=36.9°,设CD=x,分别解Rt△ACD和Rt△BCD,表示出AD、BD,再根据AD-BD=AB列出方程,解方程求出x即可.
试题解析:作CD⊥AB于D,
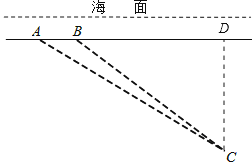
依题意,AB=500米,∠DAC=31.0°,∠CBD=36.9°,
设CD=x,
在Rt△ACD中,tan31.0°=![]() ,
,
∴AD=![]() x.
x.
在Rt△BCD中,tan36.9°=![]() ,
,
∴BD=![]() x.
x.
∵AD-BD=AB,
∴![]() x-
x-![]() x=500,
x=500,
解得x=1500,
x+500=2000.
答:海底黑匣子C所在点距离海面的深度为2000米.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

