题目内容
【题目】如图,在正方形ABCD中,AB=3cm,动点M自A点出发沿AB方向以每秒1cm的速度运动,同时动点N自A点出发沿折线AD﹣DC﹣CB以每秒3cm的速度运动,到达B点时运动同时停止.设△AMN的面积为y(cm2).运动时间为x(秒),则下列图象中能大致反映y与x之间函数关系的是( )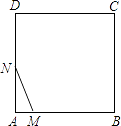
A.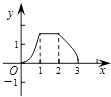
B.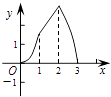
C.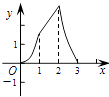
D.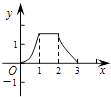
【答案】B
【解析】解:当点N在AD上时,即0≤x≤1,S△AMN= ![]() ×x×3x=
×x×3x= ![]() x2,
x2,
点N在CD上时,即1≤x≤2,S△AMN= ![]() ×x×3=
×x×3= ![]() x,y随x的增大而增大,所以排除A、D;
x,y随x的增大而增大,所以排除A、D;
当N在BC上时,即2≤x≤3,S△AMN= ![]() ×x×(9﹣3x)=﹣
×x×(9﹣3x)=﹣ ![]() x2+
x2+ ![]() x,开口方向向下.
x,开口方向向下.
故答案为:B.
这是一道分段函数的问题,分三段分析:当点N在AD上时,即0≤x≤1;点N在CD上时,即1≤x≤2;当N在BC上时,即2≤x≤3;每一段上,根据三角形的面积公式得出函数解析式,从而得出答案。

练习册系列答案
相关题目
【题目】某鞋店销售了9双鞋,各种尺码的销售量如下:
鞋的尺码 | 20 | 21 | 22 | 23 |
销售量(双) | 1 | 2 | 4 | 2 |
(1)计算这9双鞋尺码的平均数、中位数和众数.
(2)哪一个指标是鞋厂最感兴趣的指标?哪一个指标是鞋厂最不感兴趣的?