题目内容
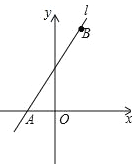
【题目】如图,已知直线l1经过点A(﹣1,0)和点B(1,4)
(1)求直线l1的表达式;
(2)若点P是x轴上的点,且△APB的面积为8,求出点P的坐标.
【答案】(1)y=2x+2(2)P(﹣5,0)或(3,0)
【解析】
(1)首先设出设直线l1的解析式为![]() ,根据待定系数法把点A(﹣1,0)和点B(1,4)代入设的解析式,即可求出一次函数的解析式;
,根据待定系数法把点A(﹣1,0)和点B(1,4)代入设的解析式,即可求出一次函数的解析式;
(2)根据三角形的面积计算出AP的长,进而得到P点坐标.
(1)设直线l1的表达式为y=kx+b(k≠0),
∵一次函数的图象经过点A(﹣1,0)和点B(1,4).
∴![]() ,解得
,解得![]() ,
,
∴直线l1的表达式为y=2x+2;
(2)∵△APB的面积为8,点B(1,4),
∴![]() ×AP×4=8,
×AP×4=8,
解得:AP=4,
∵点A(﹣1,0),
∴P(﹣5,0)或(3,0).

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目
【题目】在学校组积的科学家素养竞赛中,每班参加比赛的人数相同,成绩分为A、B、C、D四个等级,其中相应等级的得分依次记为90分、80分、70 分、60 分,学校将八年级(1)班和(2) 班的成绩整理并绘制成如下的统计图:
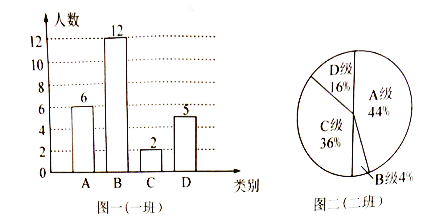
请你根据以上提供的信息解答下列问题:
(1) 此次竞赛中二 班成绩在70分以上(包括70分) 的人数有多少人?
(2) 补全下表中空缺的三个统计量:
平均数/ 分 | 中位数/ 分 | 众数/ 分 | |
一班 | 77.6 | 80 | _____________ |
二班 | _____________ | ______________ | 90 |
(3) 请根据上述图表对这次竞赛成绩进行分析,写出两个结论.