题目内容
【题目】如图,在平面直角坐标系中,等腰直角三角形ABC的腰长为2,直角顶点A在直线l:y=2x+2上移动,且斜边BC∥x轴,当△ABC在直线l上移动时,BC的中点D满足的函数关系式为( )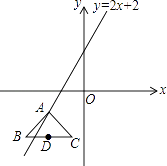
A.y=2x
B.y=2x+1
C.y=2x+2﹣ ![]()
D.y=2x﹣ ![]()
【答案】C
【解析】解:如图所示: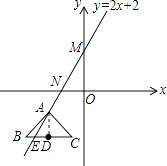
连接AD,BD交直线l:y=2x+2于点E,
∵AB=AC,D为BC的中点,
∴AD⊥BC,
∵BC∥x轴,
∴AD∥y轴,
∵y=2x+2当y=0,x=﹣1;当x=0,y=2,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∵AB=AC=2,
∴AD= ![]() ,
,
∴ED= ![]() ,
,
由题意可得点D所在直线平行于y=2x+2所在直线,
∴BC的中点D满足的函数关系式为:y=2(x﹣ ![]() )+2=2x﹣
)+2=2x﹣ ![]() +2.
+2.
故选:C.
【考点精析】解答此题的关键在于理解相似三角形的应用的相关知识,掌握测高:测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长成比例”的原理解决;测距:测量不能到达两点间的举例,常构造相似三角形求解.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目