题目内容
一个三角形两边的长分别为6和8,第三边的边长是方程(x-10)(x-6)=0的一个实数根,则这个三角形的面积是( )
| A、24 | ||
B、24或8
| ||
| C、48 | ||
D、8
|
分析:先解出方程的根,然后根据三角形的三边关系及勾股定理的逆定理解答.
解答: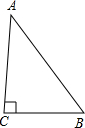 解:方程(x-10)(x-6)=0的一个实数根是10或6,
解:方程(x-10)(x-6)=0的一个实数根是10或6,
(1)∵62+82=102,根据勾股定理的逆定理,故此三角形为直角三角形;
故面积为
×6×8=24cm2,
故三角形的面积是24cm2
(2)已知AB=AC=6,BC=8,根据勾股定理: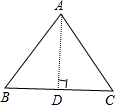
∴AD=
=2
,
∴面积为:
×2
×8=8
.
故选B.
 解:方程(x-10)(x-6)=0的一个实数根是10或6,
解:方程(x-10)(x-6)=0的一个实数根是10或6,(1)∵62+82=102,根据勾股定理的逆定理,故此三角形为直角三角形;
故面积为
| 1 |
| 2 |
故三角形的面积是24cm2
(2)已知AB=AC=6,BC=8,根据勾股定理:

∴AD=
| 62- 42 |
| 5 |
∴面积为:
| 1 |
| 2 |
| 5 |
| 5 |
故选B.
点评:本题考查勾股定理的逆定理的应用.判断三角形是否为直角三角形,已知三角形三边的长,只要利用勾股定理的逆定理加以判断即可.
勾股定理的逆定理:若三角形三边满足a2+b2=c2,那么这个三角形是直角三角形.
勾股定理的逆定理:若三角形三边满足a2+b2=c2,那么这个三角形是直角三角形.

练习册系列答案
相关题目