Question

【题目】(2016湖北襄阳第22题)

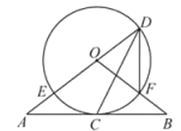
如图，直线AB经过⊙O上的点C，直线AO与⊙O交于点E和点D，OB与OD交于点F，连接DF，DC．已知OA=OB，CA=CB，DE=10，DF=6．

(1)求证：①直线AB是⊙O的切线；②∠FDC=∠EDC；

(2)求CD的长.

Answer 1

【答案】(1)详见解析；（2）.

【解析】

试题分析：(1)①连接0C，易证OC⊥AB，即可判定直线AB是⊙O的切线；②根据等腰三角形的性质可得∠AOC=∠BOC,再由圆周角定理可得，所以∠FDC=∠EDC；（2）连接EF交OC于G，连接EC，先求得EF=8，根据垂径定理得EG=FG=4,再求得OG=3，GC=2，在Rt△EGC中，根据勾股定理可得CE=，在Rt△ECD中，再由勾股定理可得CD=.

试题解析：(1)证明：①连接0C，

∵OA=OB，AC=BC，∴OC⊥AB．

∴直线AB是⊙O的切线．

(2)连接EF交OC于G，连接EC．

∵DE是直径，∴∠DFE=∠DCE=90°

在Rt△EGC中，CE=

在Rt△ECD中，CD=