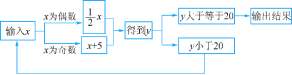
题目内容
【题目】(1)若有理数x、y,满足|x|=5,|y|=2,且|x+y|=x+y,求x-y的值.
(2)已知a和b互为相反数,c,d互为倒数,|x|=2,求3a+3b-![]() - x
- x
【答案】(1)3或7;(2)![]() 或
或![]() .
.
【解析】
(1)先去绝对值算出x、y的值,再根据|x+y|=x+y,讨论出x、y的取值,从而可以求x-y的值;
(2)根据互为相反数的两个数之和为0可得a+b=0,根据互为倒数的两个数之积为1,可得cd=1,由|x|=2可得x=±2,再带入式子即可.
解:(1)∵|x|=5,|y|=2, ∴x=±5,y=±2;
又∵|x+y|=x+y,∴x+y≥0;
∴当x=5时,y=2或-2此时x-y=5-2=3或x-y=5-(-2)=7;
当x=-5时,y=2或-2都不符合题意,舍去.
故x-y的值为3或7.
(2)∵a和b互为相反数,∴a+b=0;
∵c,d互为倒数,∴cd=1;
∵|x|=2,∴x=±2;
当x=2时,原式=![]() .
.
当x=-2时,原式=![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目