题目内容
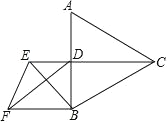
【题目】如图，在正方形ABCD中，E为边AD的中点，点F在边CD上，且CF=3FD，△ABE与△DEF相似吗？为什么？
【答案】相似
【解析】
先根据正方形的性质得∠A=∠D=90°，AB=AD=CD，设AB=AD=CD=4a，利用E为边AD的中点，CF=3FD，得到AE=DE=2a，DF=a，则可计算出
=2，加上∠A=∠D，于是根据相似三角形的判定方法即可得到△ABE∽△DEF．
△ABE与△DEF相似．理由如下：
∵四边形ABCD为正方形，
∴∠A=∠D=90°，AB=AD=CD，
设AB=AD=CD=4a，
∵E为边AD的中点，CF=3FD，
∴AE=DE=2a，DF=a，
∴
=2，
=2，
∴
=2
而∠A=∠D，
∴△ABE∽△DEF．
练习册系列答案
相关题目
