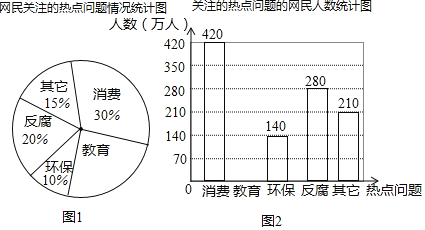
题目内容
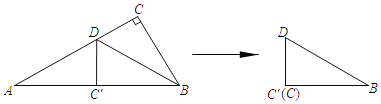
【题目】在△ABC和△ADE中,BA=BC,DA=DE,且∠ABC=∠ADE,点E在△ABC的内部,连接EC,EB和ED,设EC=kBD(k≠0).
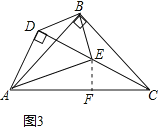
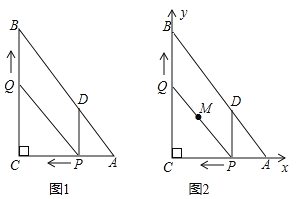
(1)当∠ABC=∠ADE=60°时,如图1,请求出k值,并给予证明;
(2)当∠ABC=∠ADE=90°时:
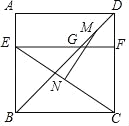
①如图2,(1)中的k值是否发生变化,如无变化,请给予证明;如有变化,请求出k值并说明理由;
②如图3,当D,E,C三点共线,且E为DC中点时,请求出tan∠EAC的值.

【答案】(1)k=1,理由见解析;(2)①k值发生变化,k=![]() ,理由见解析;②tan∠EAC=
,理由见解析;②tan∠EAC=![]() .
.
【解析】
(1)根据题意得到△ABC和△ADE都是等边三角形,证明△DAB≌△EAC,根据全等三角形的性质解答;
(2)①根据等腰直角三角形的性质、相似三角形的性质计算;
②作EF⊥AC于F,设AD=DE=a,证明△CFE∽△CAD,根据相似三角形的性质求出EF,根据勾股定理求出AF,根据正切的定义计算即可.
(1)k=1,
理由如下:如图1,∵∠ABC=∠ADE=60°,BA=BC,DA=DE,
∴△ABC和△ADE都是等边三角形,
∴AD=AE,AB=AC,∠DAE=∠BAC=60°,
∴∠DAB=∠EAC,
在△DAB和△EAC中,
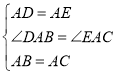 ,
,
∴△DAB≌△EAC(SAS)
∴EC=DB,即k=1;
(2)①k值发生变化,k=![]() ,
,
∵∠ABC=∠ADE=90°,BA=BC,DA=DE,
∴△ABC和△ADE都是等腰直角三角形,
∴![]() ,
,![]() ,∠DAE=∠BAC=45°,
,∠DAE=∠BAC=45°,
∴![]() ,∠DAB=∠EAC,
,∠DAB=∠EAC,
∴△EAC∽△DAB,
∴![]() ,即EC=
,即EC=![]() BD,
BD,
∴k=![]() ;
;
②作EF⊥AC于F,
设AD=DE=a,则AE=![]() a,
a,
∵点E为DC中点,
∴CD=2a,
由勾股定理得,AC=![]() ,
,
∵∠CFE=∠CDA=90°,∠FCE=∠DCA,
∴△CFE∽△CAD,
∴![]() ,即
,即![]() ,
,
解得,EF=![]() ,
,
∴AF=![]() ,
,
则tan∠EAC=![]() .
.