Question

【题目】如图，在△ABC中，∠C＝90°，AC＝8，BC＝6，点D是AB的中点，点E在AC上，将△ADE沿DE翻折，使点A落在点A′处，当A′D与△ABC的一边平行时，A′B＝____________．

Answer 1

【答案】或

【解析】

根据题意，先求出AB的长度，由折叠后，A′D与△ABC的一边平行时，可分为两种情况进行①当∥AC时；②当∥BC时；利用折叠的性质，矩形的性质，中位线定理，以及勾股定理，分别求出两种情况的长度，即可得到答案.

解：在△ABC中，∠C＝90°，AC＝8，BC＝6，

由勾股定理，得：，

∵点D是AB的中点，

∴AD=BD=5；

①当∥AC时，如图：

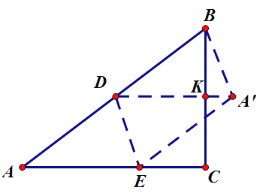
由折叠的性质，得：，

∵∥AC，点D是AB的中点，

∴点K是BC的中点，

∴，，

∴，

在Rt△中，由勾股定理，得：

；

②当∥BC时，如图：过作⊥BC于点G.

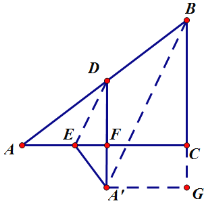
由折叠的性质，得，

∵∥BC，点D是AB的中点，

∴点F是AC的中点，

∴，，

∴，

易得四边形是矩形，

∴，，

在Rt△中，由勾股定理得：

.

故答案为：或.