题目内容
【题目】如图,在△ABC中,∠ABC=90°,以BC为直径作⊙O,交AC于D,E为 ![]() 的中点,连接CE,BE,BE交AC于F.
的中点,连接CE,BE,BE交AC于F. 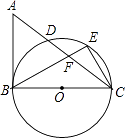
(1)求证:AB=AF;
(2)若AB=3,BC=4,求CE的长.
【答案】
(1)证明:∵E为 ![]() 的中点,
的中点,
∴ ![]() ,
,
∴∠DCE=∠CBE,
∵BC为⊙O的直径,
∴∠CEF=90°,
∴∠AFB=∠EFC=90°﹣∠DCE,
又∵∠ABF=∠ABC﹣∠CBE=90°﹣∠CBE,
∴∠ABF=∠AFB,
∴AB=AF;
(2)解:连接BD,如图所示:

∵BC为⊙O的直径,
∴∠BDC=90°,即BD⊥AC,
∵∠ABC=90°,
∴AC= ![]() =
= ![]() =5,
=5,
∵∠ADB=90°=∠ABC,∠A=∠A,
∴△ABD∽△ACB,
∴ ![]() =
= ![]() ,即
,即 ![]() ,
,
解得:AD= ![]() ,BD=
,BD= ![]() ,
,
∵AF=AB=3,
∴CF=AC﹣AF=2,DF=AF﹣AD=3﹣ ![]() =
= ![]() ,
,
∴BF= ![]() =
= ![]() ,
,
∵∠BDF=∠CEF,∠DFB=∠EFC,
∴△BDF∽△CEF,
∴ ![]() ,即
,即 ![]() ,
,
解得:CE= ![]() .
.
【解析】(1)由已知条件得出 ![]() ,由圆周角定理得出∠DCE=∠CBE,∠CEF=90°,得出∠AFB=∠EFC=90°﹣∠DCE,证出∠ABF=∠AFB,即可得出结论;(2)连接BD,由勾股定理求出AC=5,证明△ABD∽△ACB,得出对应边成比例求出AD=
,由圆周角定理得出∠DCE=∠CBE,∠CEF=90°,得出∠AFB=∠EFC=90°﹣∠DCE,证出∠ABF=∠AFB,即可得出结论;(2)连接BD,由勾股定理求出AC=5,证明△ABD∽△ACB,得出对应边成比例求出AD= ![]() ,BD=
,BD= ![]() ,由AF=AB=3,得出CF=AC﹣AF=2,DF=AF﹣AD=
,由AF=AB=3,得出CF=AC﹣AF=2,DF=AF﹣AD= ![]() ,由勾股定理求出BF,再证明△BDF∽△CEF,得出对应边成比例,即可得出结果.
,由勾股定理求出BF,再证明△BDF∽△CEF,得出对应边成比例,即可得出结果.
【考点精析】通过灵活运用圆周角定理和相似三角形的判定与性质,掌握顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方即可以解答此题.

【题目】某校八年级学生在学习《数据的分析》后,进行了检测,现将该校八(1)班学生的成绩统计如下表,并绘制成条形统计图(不完整). 
分数(分) | 人数(人) |
68 | 4 |
78 | 7 |
80 | 3 |
88 | 5 |
90 | 10 |
96 | 6 |
100 | 5 |
(1)补全条形统计图;
(2)该班学生成绩的平均数为86.85分,写出该班学生成绩的中位数和众数;
(3)该校八年级共有学生500名,估计有多少学生的成绩在96分以上(含96分)?
(4)小明的成绩为88分,他的成绩如何,为什么?