题目内容
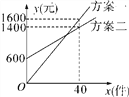
【题目】某销售公司推销一种产品,设x(件)是推销产品的数量,y(元)是付给推销员的月报酬.公司付给推销员的月报酬的两种方案如图所示,推销员可以任选一种与公司签订合同,看图解答下列问题:
(1)求每种付酬方案y关于x的函数表达式;
(2)当选择方案一所得报酬高于选择方案二所得报酬时,求x的取值范围.
【答案】(1 y=40x;y=20x+600;(2)方案一所得报酬高于方案二.
【解析】试题分析:(1)由图,已知两点,可根据待定系数法列方程,求出函数关系式;
(2)列出方程得出两直线的相交点的坐标,即可选择方案一所得报酬高于选择方案二所得报酬时x的取值范围.
试题解析:(1)设方案一的解析式为y=kx,把(40,1600)代入解析式,可得k=40,
故解析式为y=40x;
设方案二的解析式为y=ax+b,把(40,1400)和(0,600)代入解析式,
可得a=20,b=600,
故解析式为y=20x+600;
(2)根据两直线相交可得方程40x=20x+600,解得x=30.
根据两函数图象可知,当x>30时,选择方案一所得报酬高于选择方案二所得报酬.

练习册系列答案
相关题目