题目内容
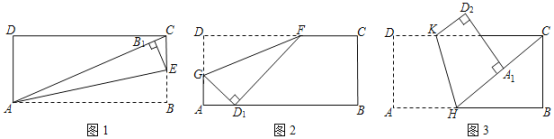
【题目】如图,点A、F、C、D在同一直线上,点B和点E分别在直线AD的两侧,且AB=DE,∠A=∠D,AF=DC.
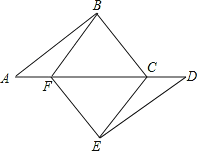
(1)求证:四边形BCEF是平行四边形,
(2)若∠ABC=90°,AB=4,BC=3,当AF为何值时,四边形BCEF是菱形.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题分析:(1)由AB=DE,∠A=∠D,AF=DC,易证得△ABC≌DEF,即可得BC=EF,且BC∥EF,即可判定四边形BCEF是平行四边形;
(2)由四边形BCEF是平行四边形,可得当BE⊥CF时,四边形BCEF是菱形,所以连接BE,交CF与点G,证得△ABC∽△BGC,由相似三角形的对应边成比例,即可求得AF的值.
试题解析:(1)证明:∵AF=DC,
∴AF+FC=DC+FC,即AC=DF.
在△ABC和△DEF中,
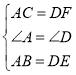 ,
,
∴△ABC≌△DEF(SAS),
∴BC=EF,∠ACB=∠DFE,
∴BC∥EF,
∴四边形BCEF是平行四边形.
(2)解:连接BE,交CF于点G,
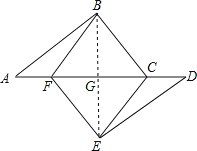
∵四边形BCEF是平行四边形,
∴当BE⊥CF时,四边形BCEF是菱形,
∵∠ABC=90°,AB=4,BC=3,
∴AC=![]() =5,
=5,
∵∠BGC=∠ABC=90°,∠ACB=∠BCG,
∴△ABC∽△BGC,
∴![]() ,
,
即![]() ,
,
∴CG=![]() ,
,
∵FG=CG,
∴FC=2CG=![]() ,
,
∴AF=AC-FC=5-![]() =
=![]() ,
,
∴当AF=![]() 时,四边形BCEF是菱形.
时,四边形BCEF是菱形.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
【题目】甲、乙二人同时从学校出发,沿同一方向匀速行走,![]() 后,甲加快速度继续匀速行走(加速的时间忽略不计),乙始终匀速行走,两人都走了
后,甲加快速度继续匀速行走(加速的时间忽略不计),乙始终匀速行走,两人都走了![]() .两人在行走过程中得到如下表所示的信息:
.两人在行走过程中得到如下表所示的信息:
离开学校的时间 |
|
|
|
|
甲离学校的距离 |
|
|
|
|
乙离学校的距离 |
|
|
|
|
(1)根据题意,甲出发时的速度为_______![]() ,乙的速度为______
,乙的速度为______![]() ;
;
(2)求表中![]() 的值.
的值.