题目内容
 20、如图,平行四边形ABCD中,G是CD上一点,BG交AD延长线于E,AF=CG,∠DGE=100度.
20、如图,平行四边形ABCD中,G是CD上一点,BG交AD延长线于E,AF=CG,∠DGE=100度.(1)试说明DF=BG;
(2)试求∠AFD的度数.
分析:(1)一组对边平行且相等的四边形是平行四边形,在本题中可知存在这一关系的是DG和BF,所以四边形DFBG为平行四边形,因此DF=BG.
(2)两直线平行,同位角相等,在本题中用到了两次此性质,可得出所求结论.
(2)两直线平行,同位角相等,在本题中用到了两次此性质,可得出所求结论.
解答:解:(1)证明:∵四边形ABCD是平行四边形,
∵AB=DC,又AF=CG,
∴AB-AF=DC-CG,即GD=BF.
又DG∥BF,
∴四边形DFBG是平行四边形,
∴DF=BG.
(2)解:∵四边形DFBG是平行四边形,
∴DF∥GB,
∴∠GBF=∠AFD.
同理可得∠GBF=∠DGE.
∠AFD=∠DGE=100°.
∵AB=DC,又AF=CG,
∴AB-AF=DC-CG,即GD=BF.
又DG∥BF,
∴四边形DFBG是平行四边形,
∴DF=BG.
(2)解:∵四边形DFBG是平行四边形,
∴DF∥GB,
∴∠GBF=∠AFD.
同理可得∠GBF=∠DGE.
∠AFD=∠DGE=100°.
点评:此题主要考查了平行四边形的判定以及平行线的性质,难易程度适中.

练习册系列答案
相关题目
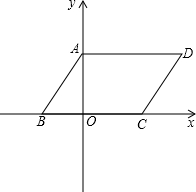 次方程x2-7x+12=0的两个根,且OA>OB.
次方程x2-7x+12=0的两个根,且OA>OB.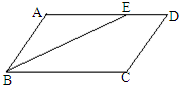 10、如图,平行四边形ABCD中,∠ABC的角平分线BE交AD于E点,AB=3,ED=1,则平行四边形ABCD的周长是
10、如图,平行四边形ABCD中,∠ABC的角平分线BE交AD于E点,AB=3,ED=1,则平行四边形ABCD的周长是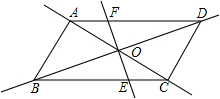
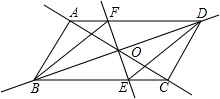
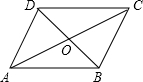 如图,平行四边形ABCD中,对角线AC和BD相交于点O,如果AC=12,BD=10,AB=m,那么m的取值范围是
如图,平行四边形ABCD中,对角线AC和BD相交于点O,如果AC=12,BD=10,AB=m,那么m的取值范围是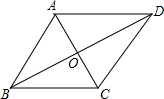 如图,平行四边形ABCD的两条对角线AC、BD相交于点O,AB=5,AC=6,DB=8,则四边形ABCD是的周长为
如图,平行四边形ABCD的两条对角线AC、BD相交于点O,AB=5,AC=6,DB=8,则四边形ABCD是的周长为