题目内容
【题目】如下图。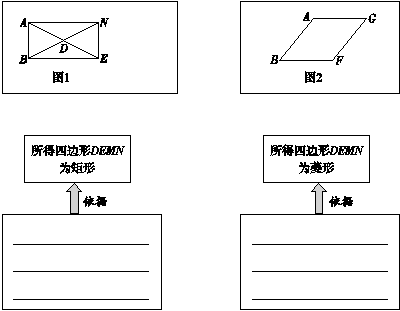
(1)画图-连线-写依据:
先分别完成以下画图(不要求尺规作图),再与判断四边形DEMN形状的相应结论连线,并写出判定依据(只将最后一步判定特殊平行四边形的依据填在横线上).
①如图1,在矩形ABEN中,D为对角线的交点,过点N画直线NP∥DE , 过点E画直线EQ∥DN , NP与EQ的交点为点M , 得到四边形DEMN;
②如图2,在菱形ABFG中,顺次连接四边AB , BF , FG , GA的中点D , E , M , N , 得到四边形DEMN.
(2)请从图1、图2的结论中选择一个进行证明.
【答案】
(1)
解:见图3,图4,连线、
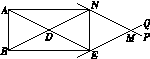
图3依据:有一组邻边相等的平行四边形为菱形.
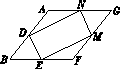
图4依据:有一个角为直角的平行四边形为矩形.
(2)
证明:①如图3.
∵ NP∥DE,EQ∥DN,NP与EQ的交点为点M,
∴ 四边形DEMN为平行四边形.
∵ D为矩形ABEN对角线的交点,
∴ AE=BN, ![]() ,
, ![]() .
.
∴ DE= DN.
∴ 平行四边形DEMN是菱形.
②如图5,连接AF,BG,记交点为H.
∵ D,N两点分别为AB,GA边的中点,
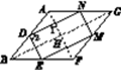
图5
∴ DN∥BG, ![]() .
.
同理,EM∥BG, ![]() ,DE∥AF,
,DE∥AF, ![]() .
.
∴ DN∥EM,DN=EM.
∴ 四边形DEMN为平行四边形.
∵ 四边形ABFG是菱形,
∴ AF⊥BG.
∴ ![]() .
.
∴ ![]() .
.
∴ ![]() .
.
∴ 平行四边形DEMN是矩形
【解析】(1)如图3,依据为有一组邻边相等的平行四边形为菱形.如图4依据为有一个角为直角的平行四边形为矩形.
(2)①如图3.由NP∥DE,EQ∥DN得 四边形DEMN为平行四边形;根据DE= DN得到平行四边形DEMN是菱形.
②如图5,连接AF , BG , 记交点为H.由 D , N、E、M为中点得DN∥EM , DN=EM.所以四边形DEMN为平行四边形.由菱形得![]() =
=![]()
![]()
所以 平行四边形DEMN是矩形。

 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案

