��Ŀ����
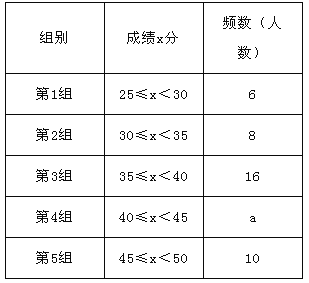
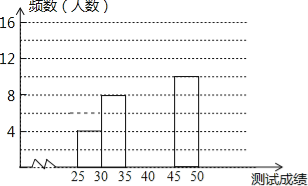
����Ŀ����ͼ1��ʾ����A��B����֮��������վCվ���ͳ���A��ʻ��Cվ��������B��ʻ��A�أ�����ͬʱ������������ʻ��ͼ2�ǿͳ���������Cվ��·��y1 �� y2��ǧ�ף�����ʻʱ��x��Сʱ��֮��ĺ�����ϵͼ��
��1����գ�A��B�������ǧ�ף�
��2������Сʱ������Cվ��·��y2����ʻʱ��x֮��ĺ�����ϵʽ��
��3���͡���������ʱ��������������Cվ��·���Ƕ���ǧ�ף�
���𰸡�
��1��420
��2���⣺��ͼ��֪�������ٶ�Ϊ60��2=30ǧ��/Сʱ��
��������A��һ����Ҫ2+360��30=14Сʱ��
��y2=kx+b������㣨2��0������14��360����
![]() ��
��
���k=30��b=-60 ��y2=30x-60����x��2��
��3���⣺��ͳ���Cվ��·��y1����ʻʱ��x֮��ĺ�������ʽΪy1=k1x+b1�����������
![]()
���k1=-60��b1=360 y1=-60x+360 ��y1=y2�� 30x-60=-60x+360 ���x= ![]()
![]() ��ǧ�ף�
��ǧ�ף�
�𣺿͡��������ڳ����� ![]() Сʱ��������������Cվ��·����80ǧ��.
Сʱ��������������Cվ��·����80ǧ��.
���������⣺��1���������֪��B��C֮��ľ���Ϊ60ǧ�ף�A��C֮��ľ���Ϊ360ǧ�ף�����A��B�������360+60=420ǧ�ף�
��1����y���ϵij�ʼֵ����֪������Cվ�ľ��룬������ӣ�����A��B���صľ��룻��2��DP�ε�һ�κ���ͼ���ô���ϵ�������;(3)������ʱ�����DP ����ͳ�ͼ��Ľ��������.

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�