题目内容
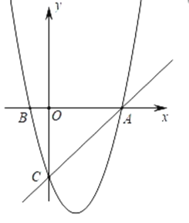
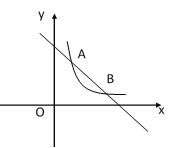
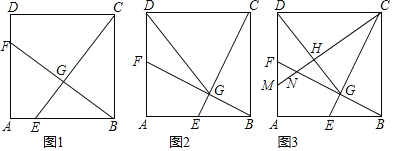
【题目】如图1,在正方形ABCD中,点E是AB边上的一个动点(点E与点A,B不重合),连接CE,过点B作BF⊥CE于点G,交AD于点F.
(1)求证:![]() ;
;
(2)如图2,当点E运动到AB中点时,连接DG,求证:DC=DG;
(3)如图3,在(2)的条件下,过点C作CM⊥DG于点H,分别交AD,BF于点M,N,求![]() 的值.
的值.
【答案】(1)见解析;(2)见解析;(3)![]() .
.
【解析】
(1)先判断出![]() ,再由四边形
,再由四边形![]() 是正方形,得出
是正方形,得出![]() ,
,![]() ,即可得出结论;
,即可得出结论;
(2)过点![]() 作
作![]() 于
于![]() ,设
,设![]() ,先求出
,先求出![]() ,进而得出
,进而得出![]() ,再求出
,再求出![]() ,
,![]() ,再判断出
,再判断出![]() ,进而判断出
,进而判断出![]() ,即可得出结论;
,即可得出结论;
(3)先求出![]() ,再求出
,再求出![]() ,再判断出
,再判断出![]() ,求出
,求出![]() ,再用勾股定理求出
,再用勾股定理求出![]() ,最后判断出
,最后判断出![]() ,得出
,得出![]() ,即可得出结论.
,即可得出结论.
(1)证明:∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵四边形![]() 是正方形,
是正方形,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;
(2)证明:如图2,过点![]() 作
作![]() 于
于![]() ,
,
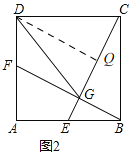
设![]() ,
,
∵点![]() 是
是![]() 的中点,
的中点,
∴![]() ,
,
∴![]() ,
,
在![]() 中,根据面积相等,得
中,根据面积相等,得![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ;
;
(3)解:如图3,过点![]() 作
作![]() 于
于![]() ,
,
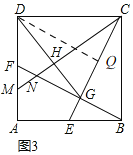
![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴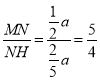

练习册系列答案
相关题目