题目内容
【题目】在等腰Rt△ABC中,∠ACB=90°,AC=BC,点D是BC边上一点,BN⊥AD交AD的延长线于点N. 
(1)如图1,若CM∥BN交AD于点M.
①直接写出图1中所有与∠MCD相等的角:;(注:所找到的相等关系可以直接用于第②小题的证明过程
②过点C作CG⊥BN,交BN的延长线于点G,请先在图1中画出辅助线,再回答线段AM、CG、BN有怎样的数量关系,并给予证明 .
(2)如图2,若CM∥AB交BN的延长线于点M.请证明:∠MDN+2∠BDN=180°.
【答案】
(1)∠CAD,∠CBN;在图1中画出图形,如图所示, 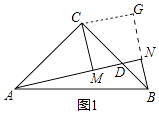
结论:AM=CG+BN,
证明:在△ACM和△BCG中,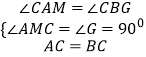 ,
,
∴△ACM≌△BCG,
∴CM=CG,AM=BG,
∵∠CMN=∠MNG=∠G=90°,
∴四边形MNGC是矩形,
∴CM=GN=CG,
∴AM=BG=BN+GN=BN+CG
(2)解:过点C作CE平分∠ACB,交AD于点E.

∵在△ACD和△BDN中,∠ACB=90°,AN⊥ND
∴∠4+∠ADC=90°=∠5+∠BDN
又∵∠ADC=∠BDN
∴∠4=∠5,
∵∠ACB=90°,AC=BC,CE平分∠ACB,
∴∠6=45°,∠2=∠3=45°
又∵CM∥AB,
∴∠1=∠6=45°=∠2=∠3,
在△ACE和△BCM中,
 ,
,
∴△ACE≌△BCM(ASA)
∴CE=CM
又∵∠1=∠2,CD=CD
∴∠CDE=∠CDM
又∵∠BDN=∠CDE,∠MDN+∠CDE+∠CDM=180°
∴∠MDN+2∠BDN=180°
【解析】解:(1)①∵CM∥BN,BN⊥AN,
∴∠CMD=∠N=90°,∠MCD=∠CBN,
∵∠ACB=90°,
∴∠ACM+∠CAD=90°,∠MCD+∠ACM=90°,
∴∠MCD=∠CAD,
所以答案是∠CAD、∠CBN.
②在图1中画出图形,如图所示,
结论:AM=CG+BN,
证明:在△ACM和△BCG中,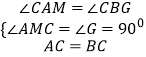 ,
,
∴△ACM≌△BCG,
∴CM=CG,AM=BG,
∵∠CMN=∠MNG=∠G=90°,
∴四边形MNGC是矩形,
∴CM=GN=CG,
∴AM=BG=BN+GN=BN+CG.
【考点精析】认真审题,首先需要了解等腰直角三角形(等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°).


