题目内容
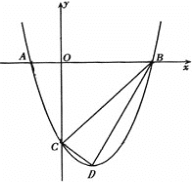
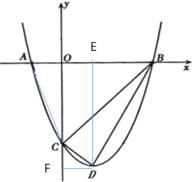
【题目】如图,抛物线与x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C(0,-3),设抛物线的顶点为D.
(1)求该抛物线的解析式与顶点D的坐标;
(2)以B、C、D为顶点的三角形是直角三角形吗?为什么?
(3)设(1)中的抛物线上有一个动点P,当点P在该抛物线上滑动到什么位置时,满足S△PAB=8,并求出此时P点的坐标.
【答案】(1)y=x2-2x-3 顶点是(1,-4);(2)直角三角形;(3)点P在该抛物线上滑动至(![]() ,4)或(
,4)或(![]() ,4)或(1,-4)时,满足S⊿PAB=8.
,4)或(1,-4)时,满足S⊿PAB=8.
【解析】
(1)设抛物线的解析式为y=ax2+bx+c,把A、B、C、三点坐标代入求出a、b、c的值即可得答案.(2)过点D分别作x轴、y轴的垂线,垂足分别为E、F,根据B、C、D三点的坐标可求出BD、CD、BC的长,根据三边的长即可判断△BCD的形状.(3)设P的纵坐标为![]() ,利用三角形面积可求出P点的纵坐标,代入解析式可求出横坐标即可.
,利用三角形面积可求出P点的纵坐标,代入解析式可求出横坐标即可.
(1)设抛物线解析式为y=ax2+bx+c
∴依题意得: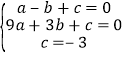 解得
解得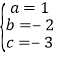
∴抛物线解析式为:y=x2-2x-3 顶点是(1,-4)
(2)以B、C、D为顶点的三角形是直角三角形。
过点D分别作x轴、y轴的垂线,垂足分别为E、F
在Rt⊿BOC中,OB=3,OC=3,
∴BC2=18
在Rt⊿CDF中,DF=1,CF=OF-OC=4-3=1
CD2=2
在Rt⊿BDE中,DE=4,BE=OB-OE=3-1=2,
∴BD2=20
∴BC2+CD2=BD2,故⊿BCD为直角三角形。
(3)设P的纵坐标为![]()
∵S⊿PAB=8
∴![]() AB·
AB·![]() =8
=8
∵AB=3+1=4
∴![]() =4
=4
∴yp=![]()
把yp=4代入解析式得4=x2-2x-3,解得:x=![]()
把yp=-4代入解析式得-4=x2-2x-3,解得:x=1
∴点P在该抛物线上滑动至(![]() ,4)或(
,4)或(![]() ,4)或(1,-4)时,满足S⊿PAB=8
,4)或(1,-4)时,满足S⊿PAB=8