题目内容
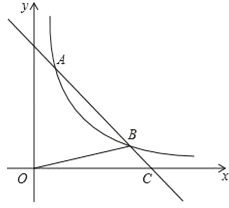
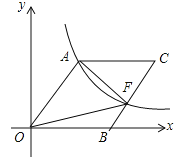
【题目】如图,O为坐标原点,四边形OACB是菱形,OB在x轴的正半轴上,sin∠AOB=![]() ,反比例函数
,反比例函数![]() 在第一象限内的图象经过点A,与BC交于点F,则△AOF的面积等于( )
在第一象限内的图象经过点A,与BC交于点F,则△AOF的面积等于( )
A.60 B.80 C.30 D.40
【答案】D.
【解析】
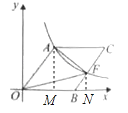
试题分析:过点A作AM⊥x轴于点M,过点F作FN⊥x轴于点N,如图所示.
设OA=a,BF=b,在Rt△OAM中,∠AMO=90°,OA=a,sin∠AOB=![]() ,∴AM=OAsin∠AOB=
,∴AM=OAsin∠AOB=![]() a,OM=
a,OM=![]() =
=![]() a,∴点A的坐标为(
a,∴点A的坐标为(![]() a,
a,![]() a).∵点A在反比例函数
a).∵点A在反比例函数![]() 的图象上,∴
的图象上,∴![]() a×
a×![]() a=
a=![]() =48,解得:a=10,或a=﹣10(舍去),∴AM=8,OM=6.∵四边形OACB是菱形,∴OA=OB=10,BC∥OA,∴∠FBN=∠AOB.在Rt△BNF中,BF=b,sin∠FBN=
=48,解得:a=10,或a=﹣10(舍去),∴AM=8,OM=6.∵四边形OACB是菱形,∴OA=OB=10,BC∥OA,∴∠FBN=∠AOB.在Rt△BNF中,BF=b,sin∠FBN=![]() ,∠BNF=90°,∴FN=BFsin∠FBN=
,∠BNF=90°,∴FN=BFsin∠FBN=![]() b,BN=
b,BN=![]() =
=![]() b,∴点F的坐标为(10+
b,∴点F的坐标为(10+![]() b,
b,![]() b).
b).
∵点B在反比例函数![]() 的图象上,∴(10+
的图象上,∴(10+![]() b)×
b)×![]() b=48,解得:b=
b=48,解得:b=![]() ,或b=
,或b=![]() (舍去),∴FN=
(舍去),∴FN=![]() ,BN=
,BN=![]() ,MN=OB+BN﹣OM=
,MN=OB+BN﹣OM=![]() .
.
S△AOF=S△AOM+S梯形AMNF﹣S△OFN=S梯形AMNF=![]() (AM+FN)MN=
(AM+FN)MN=![]() (8+
(8+![]() )×(
)×(![]() )=40.故选D.
)=40.故选D.

练习册系列答案
相关题目