题目内容
【题目】Rt△ABC中,∠C=90°,点D、E是△ABC边AC、BC上的点,点P是一动点.令∠PDA=∠1,∠PEB=∠2,∠DPE=∠α. 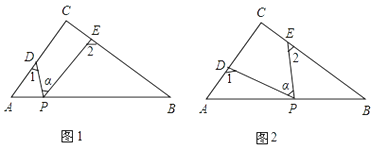
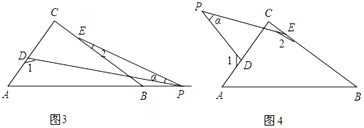
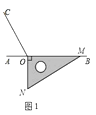
(1)若点P在线段AB上,如图(1),∠α=50°,则∠1+∠2=°
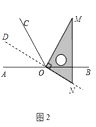
(2)若点P在边AB上运动,如图(2)所示,则∠α、∠1、∠2之间的关系为:
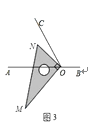
(3)若点P运动到边AB的延长线上,如图(3)所示,则∠α、∠1、∠2之间有何关系?猜想并说明理由.
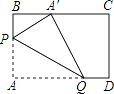
(4)若点P运动到△ABC形外,如图(4),则∠α、∠1、∠2之间的关系为: .
【答案】
(1)140
(2)∠1+∠2=90°+α
(3)解:∠1=90°+∠2+α,
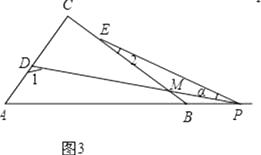
理由:如图3,∵∠2+∠α=∠DME,∠DME+∠C=∠1,
∴∠1=∠C+∠2+α=90°+∠2+α
(4)∠2=90°+∠1﹣α
【解析】解:(1.)∵∠1+∠2+∠CDP+∠CEP=360°,∠C+∠α+∠CDP+∠CEP=360°, ∴∠1+∠2=∠C+∠α,
∵∠C=90°,∠α=50°,
∴∠1+∠2=140°,
所以答案是:140;
(2.)∵∠1+∠2+∠CDP+∠CEP=360°,∠C+∠α+∠CDP+∠CEP=360°,
∴∠α+∠C=∠1+∠2,
∴∠1+∠2=90°+α,
所以答案是:∠1+∠2=90°+α;
(4.)如图4,∵∠PFD=∠EFC,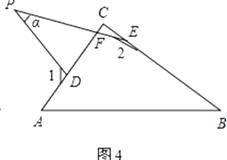
∴180°﹣∠PFD=180°﹣∠EFC,
∴∠α+180°﹣∠1=∠C+180°﹣∠2,
∴∠2=90°+∠1﹣α,
所以答案是:∠2=90°+∠1﹣α.
【考点精析】利用三角形的内角和外角和三角形的外角对题目进行判断即可得到答案,需要熟知三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角;三角形一边与另一边的延长线组成的角,叫三角形的外角;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角.

 名校课堂系列答案
名校课堂系列答案