题目内容
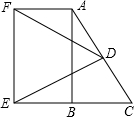 Rt△ABC中,∠ABC=90°,∠C=60°,BC=2,D是AC的中点,从D作DE⊥AC与CB的延长线交于点E,以AB、BE为邻边作矩形ABEF,连接DF,则DF的长是
Rt△ABC中,∠ABC=90°,∠C=60°,BC=2,D是AC的中点,从D作DE⊥AC与CB的延长线交于点E,以AB、BE为邻边作矩形ABEF,连接DF,则DF的长是
- A.4

- B.3

- C.2

- D.4
C
分析:首先求证△DEC≌△BAC,得DE=AB,再求证DF=DE即可解此题.
解答:∵△ABC为直角三角形,∠C=60°,
∴∠BAC=30°,
∴BC= AC,
AC,
∵D为AC的中点,
∴BC=DC,
∴在△DEC≌△BAC中,
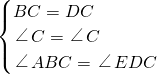
∴△DEC≌△BAC,
即AB=DE,∠DEB=30°,
∴∠FED=60°,
∵EF=AB,∴EF=DE,
∴△DEF为等边三角形,
即DF=AB,
在直角三角形ABC中,BC=2,则AC=4,
∴DF=AB= =2
=2 ,
,
故选C.
点评:本题考查了等腰三角形各边均相等,考查了矩形内角均为直角的性质,本题中求证△DEF是等边三角形是解题的关键.
分析:首先求证△DEC≌△BAC,得DE=AB,再求证DF=DE即可解此题.
解答:∵△ABC为直角三角形,∠C=60°,
∴∠BAC=30°,
∴BC=
 AC,
AC,∵D为AC的中点,
∴BC=DC,
∴在△DEC≌△BAC中,
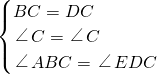
∴△DEC≌△BAC,
即AB=DE,∠DEB=30°,
∴∠FED=60°,
∵EF=AB,∴EF=DE,
∴△DEF为等边三角形,
即DF=AB,
在直角三角形ABC中,BC=2,则AC=4,
∴DF=AB=
 =2
=2 ,
,故选C.
点评:本题考查了等腰三角形各边均相等,考查了矩形内角均为直角的性质,本题中求证△DEF是等边三角形是解题的关键.

练习册系列答案
相关题目
 延长线上,且AF=CE.求证:四边形ACEF是菱形.
延长线上,且AF=CE.求证:四边形ACEF是菱形.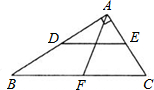 如图,在Rt△ABC中,∠BAC=90°,点D、E、F分别是三边的中点,且CF=3cm,则DE=
如图,在Rt△ABC中,∠BAC=90°,点D、E、F分别是三边的中点,且CF=3cm,则DE=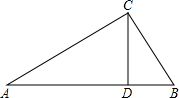 如图,Rt△ABC中,AC⊥BC,CD⊥AB于D,AC=8,BC=6,则AD=
如图,Rt△ABC中,AC⊥BC,CD⊥AB于D,AC=8,BC=6,则AD=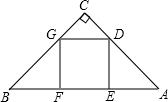 点G在边BC上.
点G在边BC上.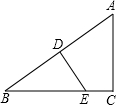 如图,Rt△ABC中,∠C=90°,D为AB的中点,DE⊥AB,AB=20,AC=12,则四边形ADEC的面积为
如图,Rt△ABC中,∠C=90°,D为AB的中点,DE⊥AB,AB=20,AC=12,则四边形ADEC的面积为