Question

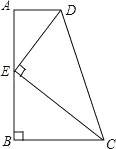
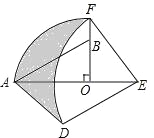
【题目】如图，在Rt△AOB中，∠AOB=90°，OA=3，OB=2，将Rt△AOB绕点O顺时针旋转90°后得Rt△FOE，将线段EF绕点E逆时针旋转90°后得线段ED，分别以O，E为圆心，OA、ED长为半径画弧AF和弧DF，连接AD，则图中阴影部分面积是（ ）

A．π B． C．3+π D．8﹣π

Answer 1

【答案】D.

【解析】

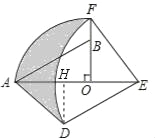
试题分析：作DH⊥AE于H，已知∠AOB=90°，OA=3，OB=2，根据勾股定理求出AB=，由旋转的性质可知，OE=OB=2，DE=EF=AB=，△DHE≌△BOA，所以DH=OB=2，所以阴影部分面积=△ADE的面积+△EOF的面积+扇形AOF的面积﹣扇形DEF的面积=×5×2+×2×3+﹣

=8﹣π，故答案选D．