题目内容
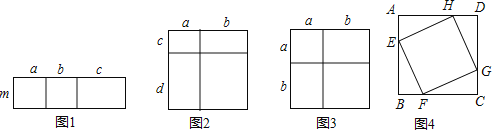
【题目】我们在学习《从面积到乘法公式》时,曾用两种不同的方法计算同一个图形的面积,探索了单项式乘多项式的运算法则:m(a+b+c)=ma+mb+mc(如图1),多项式乘多项式的运算法则:
(a+b)(c+d)=ac+ad+bc+bd(如图2),以及完全平方公式:(a+b)2=a2+2ab+b2(如图3).
把几个图形拼成一个新的图形,通过图形面积的计算,常常可以得到一些等式,这是研究数学问题的一种常用方法.
(1)请设计两个图形说明一下两个等式成立(画出示意图,并标上字母)
①(a+b)(2a+b)=2a2+3ab+b2
②(a+b+c)2=a2+b2+c2+2ab+2ac+2bc
(2)如图4,它是由四个形状、大小完全相同的直角三角形与中间的小正方形EFGH拼成的一个大正方形ABCD.如果每个直角三角形的较短的边长为a,较长的边长为b,最长的边长为c.试用两种不同的方法计算这个大正方形的面积,你能发现直角三角形的三边长a、b、c的什么数量关系?(注:写出解答过程)
【答案】(1)①如图1,见解析;②如图2,见解析;(2)a2+b2=c2.
【解析】
(1)①根据图1、图2、图3类比画出即可;
②由题意可得图形为边长是a+b+c的正方形;
(2)先求出小正方形和四个三角形的面积并求和,再用正方形公式求大正方形的面积,然后根据面积相等列出等式,最后化简即可解答.
解:(1)①如图1,(a+b)(2a+b)=2a2+3ab+b2,

②如图2,(a+b+c)2=a2+b2+c2+2ab+2ac+2bc,

(2)如图4,小正方形的面积=c2﹣![]() ab×4=c2﹣2ab=(b﹣a)2,
ab×4=c2﹣2ab=(b﹣a)2,
即a2+b2=c2.

练习册系列答案
相关题目