题目内容
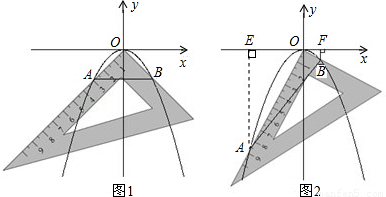
如图,将一把直角三角板的直角顶点置于平面直角坐标系的原点O,两直角边与抛物线y=ax2(a<0)交于A、B两点,请解答以下问题:
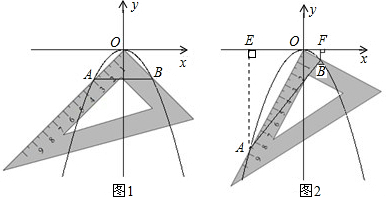
(1)若测得OA=OB=2
(如图1),求a的值;
(2)对同一条抛物线,将三角板绕点O旋转到如图2所示位置时,过B作BF⊥x轴于点F,测得OF=1,写出此时点B的坐标,并求点A的横坐标;
(3)对该抛物线,将三角板绕点O旋转任意角度时,交点A、B的连线段总经过一个固定的点,试求出该点的坐标.

(1)若测得OA=OB=2
| 2 |
(2)对同一条抛物线,将三角板绕点O旋转到如图2所示位置时,过B作BF⊥x轴于点F,测得OF=1,写出此时点B的坐标,并求点A的横坐标;
(3)对该抛物线,将三角板绕点O旋转任意角度时,交点A、B的连线段总经过一个固定的点,试求出该点的坐标.
分析:(1)根据抛物线的对成性,先求出B点坐标,代入抛物线y=ax2(a<0)得a的值;
(2)过点A作AE⊥x轴于点E,可利用AB2=OA2+OB2,求出点A的横坐标.
(3)首先设A(-m,-
m2)(m>0),B(n,-
n2)(n>0),表示出直线AB解析式中b=-
mn,再利用勾股定理得出mn=4,进而得出直线AB恒过其与y轴的交点C(0,-2).
(2)过点A作AE⊥x轴于点E,可利用AB2=OA2+OB2,求出点A的横坐标.
(3)首先设A(-m,-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:(1)设线段AB与y轴的交点为C,由抛物线的对称性可得C为AB中点,
∵OA=OB=2
,∠AOB=90°,
∴AC=OC=BC=2,∴B(2,-2),
将B(2,-2)代入抛物线y=ax2(a<0)得,a=-
.
(2)过点A作AE⊥x轴于点E,
∵点B的横坐标为1,∴B (1,-
),
设A(-m,-
m 2)(m>0),则
OB2=12+(
)2=
,OA2=m2+
m4,AB2=(1+m)2+(-
+
m2)2,
∵∠AOB=90°,∴AB2=OA2+OB2,
∴(1+m)2+(-
+
m2)2=m2+
m4+
,
解得:m=0(不合题意舍去)或m=4,即点A的横坐标为-4.
(3)解法一:设A(-m,-
m 2)(m>0),B(n,-
n 2)(n>0),
设直线AB的解析式为:y=kx+b,则
,
①×n+②×m得,(m+n)b=-
(m2n+mn2)=-
mn(m+n),
∴b=-
mn,
由前可知,OB2=n2+
n4,OA2=m2+
m4,AB2=(n+m)2+(-
m2+
n2)2,
由AB2=OA2+OB2,得:n2+
n4+m2+
m4=(n+m)2+(-
m2+
n2)2,
化简,得mn=4.
∴b=-
×4=-2.由此可知不论k为何值,直线AB恒过点(0,-2),
解法二:设A(-m,-
m 2)(m>0),B(n,-
n 2)(n>0),
直线AB与y轴的交点为C,根据S△AOB=S梯形ABFE-S△AOE-S△BOF=S△AOC+S△BOC,可得
×(
m2+
n2)(m+n)-
m×
m2-
n×
n2=
CO•m+
CO•n
化简,得CO=
mn,
由前可知,OB2=n2+
n4,OA2=m2+
m4,AB2=(n+m)2+(-
m2+
n2)2,
由AB2=OA2+OB2,得:n2+
n4+m2+
m4=(n+m)2+(-
m2+
n2)2,
化简,得mn=4.
∴OC=2为固定值.故直线AB恒过其与y轴的交点C(0,-2).
∵OA=OB=2
| 2 |
∴AC=OC=BC=2,∴B(2,-2),
将B(2,-2)代入抛物线y=ax2(a<0)得,a=-
| 1 |
| 2 |
(2)过点A作AE⊥x轴于点E,
∵点B的横坐标为1,∴B (1,-
| 1 |
| 2 |
设A(-m,-
| 1 |
| 2 |
OB2=12+(
| 1 |
| 2 |
| 5 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
∵∠AOB=90°,∴AB2=OA2+OB2,
∴(1+m)2+(-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 5 |
| 4 |
解得:m=0(不合题意舍去)或m=4,即点A的横坐标为-4.
(3)解法一:设A(-m,-
| 1 |
| 2 |
| 1 |
| 2 |
设直线AB的解析式为:y=kx+b,则
|
①×n+②×m得,(m+n)b=-
| 1 |
| 2 |
| 1 |
| 2 |
∴b=-
| 1 |
| 2 |
由前可知,OB2=n2+
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
由AB2=OA2+OB2,得:n2+
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
化简,得mn=4.

∴b=-
| 1 |
| 2 |
解法二:设A(-m,-
| 1 |
| 2 |
| 1 |
| 2 |
直线AB与y轴的交点为C,根据S△AOB=S梯形ABFE-S△AOE-S△BOF=S△AOC+S△BOC,可得
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
化简,得CO=
| 1 |
| 2 |
由前可知,OB2=n2+
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
由AB2=OA2+OB2,得:n2+
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
化简,得mn=4.
∴OC=2为固定值.故直线AB恒过其与y轴的交点C(0,-2).
点评:此题考查了抛物线的对称性和勾股定理以及一元二次方程解法,第(3)问求出mn=4是解题的关键,综合性较强,有一定的难度.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
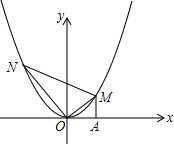 ,设M、N的横坐标分别为m、n(m>0,n<0);请解答下列问题:
,设M、N的横坐标分别为m、n(m>0,n<0);请解答下列问题: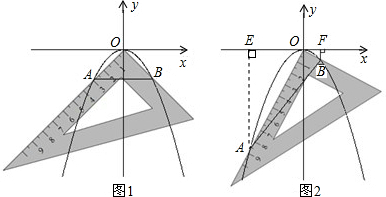
 (如图1),求a的值;
(如图1),求a的值; 交于M、N两点,设M、N的横坐标分别为m、n(m﹥0,n﹤0);请解答下列问题:
交于M、N两点,设M、N的横坐标分别为m、n(m﹥0,n﹤0);请解答下列问题: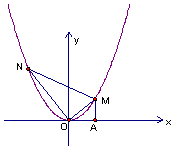
 (如图1),求a的值;
(如图1),求a的值;