题目内容
已知抛物线y=ax2+bx+c经过A(-1,0)、B(3,0)、C(0,3)三点.

(1)求抛物线的解析式和顶点M的坐标,并在给定的直角坐标系中画出这条抛物线.
(2)若点(x0,y0)在抛物线上,且0≤x0≤4,试写出y0的取值范围.
(3)设平行于y轴的直线x=t交线段BM于点P(点P能与点M重合,不能与点B重合)交x轴于点Q,四边形AQPC的面积为S.
①求S关于t的函数关系式以及自变量t的取值范围;
②求S取得最大值时点P的坐标;
③设四边形OBMC的面积为![]() ,试判断是否存在点P,使得S=
,试判断是否存在点P,使得S=![]() ,若存在,求出点P的坐标;若不存在,请说明理由.
,若存在,求出点P的坐标;若不存在,请说明理由.
解析:
|
解:(1)依题意,得方程组 解得a=-1,b=2,c=3. ∴抛物线的解析式为y=-x2+2x+3,顶点坐标为M(1,4);图象略. (2)利用图象可得,在0≤x0≤4的范围内,
当x0=4时,y0最小=-5;当x0=1时,y0最大=4∴-5≤y0≤4. (3)①S四边形AQPC=S△AOC+S梯形OQPC S△AOC= ∵点B、M坐标分别为B(3,0),M(1,4) ∴可求得线段BM所在直线解析式为y=-2x+6 ∴当x=t,y=-2t+6 ∴点P、Q坐标分别为P(t,-2t+6),Q(t,0) ∴S梯形OQPC= S四边形AQPC=-t2+ ∵点P能与点M重合,不能与点B重合∴1≤t<3 ∴S=-t2+ ②当t= ③过点M作MN⊥x轴,垂足为点N.
∴S/=S△BMN+S梯形OCMN = 若S= ∵Δ=81-96<0,方程无实数解 ∴不存在点P,使得S= |

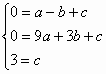
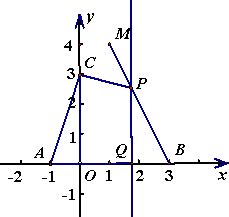
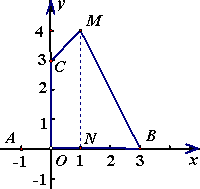
 (3)在(2)的结论下,直线x=1上是否存在点M,使△MPQ为等腰三角形?若存在,请求出所有点M的坐
(3)在(2)的结论下,直线x=1上是否存在点M,使△MPQ为等腰三角形?若存在,请求出所有点M的坐 (3)设点P为抛物线的对称轴x=1上的一动点,求使∠PCB=90°的点P的坐标.
(3)设点P为抛物线的对称轴x=1上的一动点,求使∠PCB=90°的点P的坐标.

 轴,交直线BC于点F,求线段DF的长,并求△BCD的面积;
轴,交直线BC于点F,求线段DF的长,并求△BCD的面积;