题目内容
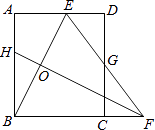
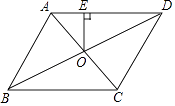
【题目】如图,直线l1经过过点P(2,2),分别交x轴、y轴于点A(4,0),B。
(1)求直线l1的解析式;
(2)点C为x轴负半轴上一点,过点C的直线l2:![]() 交线段AB于点D。
交线段AB于点D。
如图1,当点D恰与点P重合时,点Q(t,0)为x轴上一动点,过点Q作QM⊥x轴,分别交直线l1、l2于点M、N。若![]() ,MN=2MQ,求t的值;
,MN=2MQ,求t的值;
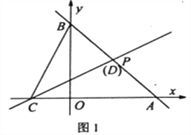
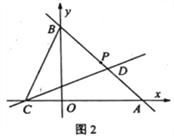
如图2,若BC=CD,试判断m,n之间的数量关系并说明理由。
【答案】(1) ![]() ;(2)①
;(2)①![]() ,
,![]() ;②
;②![]()
【解析】(1)用待定系数法求解;(2)点Q的位置有两种情况:当点Q在点A左侧,点P的右侧时![]() ;当点Q在点P的右侧时,
;当点Q在点P的右侧时,![]() .都有
.都有![]() ,再根据MN=2MQ,可求t的值;(3)由BC=CD,证△BCO≌△CDE,设C(a,0),D(4+a,-a),并代入解析式,通过解方程组可得.
,再根据MN=2MQ,可求t的值;(3)由BC=CD,证△BCO≌△CDE,设C(a,0),D(4+a,-a),并代入解析式,通过解方程组可得.
解:(1)设直线l1的解析式为y=kx+b,
直线![]() 经过点P(2,2),A(4,0),
经过点P(2,2),A(4,0),
即![]() , 解得
, 解得![]() ,
,
直线l1的解析式为y=-x+4;
(2)①∵直线l2过点P(2,2)且![]() ,
,
即直线l2:![]() ,
,
点Q(t,0),M(t,4-t),N(t,![]() ),
),
1. 当点Q在点A左侧,点P的右侧时,
![]() ,
,![]() ,
,
即![]() ,解得
,解得![]() ;
;
⒉ 当点Q在点A右侧时
![]() ,MQ=t-4,
,MQ=t-4,
即![]() ,解得t=10,
,解得t=10,

②过点D作DE⊥AC于E ,
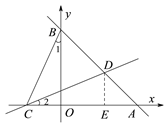
∵BC=CD,BO=OA,
∠DBC=∠1+∠ABO=∠BDC=∠2+∠DAE,
∴∠1=∠2,
∴△BCO≌△CDE,
∴OC=ED,BO=CE,
设C(a,0),D(4+a,-a),
则![]() ,
,
解得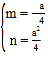 ,
,
即![]()

练习册系列答案
相关题目