题目内容
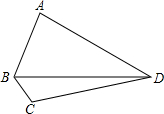 在四边形ABCD中,AB=30,AD=48,BC=14,CD=40,∠ABD+∠BDC=90°,则四边形ABCD的面积为
在四边形ABCD中,AB=30,AD=48,BC=14,CD=40,∠ABD+∠BDC=90°,则四边形ABCD的面积为936
936
.分析:作∠ABD=∠A′DB,AB=A′D,连接A′C,进而得出∠A′DB+∠BDC=90°,利用勾股定理得出A′C的长,再利用勾股定理的逆定理得出△BCA′是直角三角形,即可得出四边形ABCD的面积.
解答: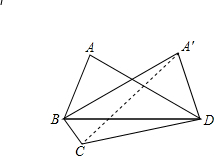 解:作∠ABD=∠A′DB,AB=A′D,连接A′C,
解:作∠ABD=∠A′DB,AB=A′D,连接A′C,
∵∠ABD+∠BDC=90°,
∴∠A′DB+∠BDC=90°,
∵AB=30,CD=40,
∴A′C=
=50,
∵AD=48,BC=14,
∴AD2+BC2=2500,
∴AD2+BC2=A′C2,
∴△BCA′是直角三角形,
∴四边形ABCD的面积为:
×30×40+
×14×48=936.
故答案为:936.
 解:作∠ABD=∠A′DB,AB=A′D,连接A′C,
解:作∠ABD=∠A′DB,AB=A′D,连接A′C,∵∠ABD+∠BDC=90°,
∴∠A′DB+∠BDC=90°,
∵AB=30,CD=40,
∴A′C=
| 302+402 |
∵AD=48,BC=14,
∴AD2+BC2=2500,
∴AD2+BC2=A′C2,
∴△BCA′是直角三角形,
∴四边形ABCD的面积为:
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:936.
点评:此题主要考查了勾股定理以及逆定理,正确将图形变形得出是解题关键.

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
 11、如图所示,在四边形ABCD中,BD是它的一条对角线,若∠1=∠2,∠A=55°16′,则∠ADC=
11、如图所示,在四边形ABCD中,BD是它的一条对角线,若∠1=∠2,∠A=55°16′,则∠ADC=
 如图,在四边形ABCD中,AD=BC,P是对角线BD的中点,M是边DC的中点,N是边AB的中点.△MPN是什么三角形?为什么?
如图,在四边形ABCD中,AD=BC,P是对角线BD的中点,M是边DC的中点,N是边AB的中点.△MPN是什么三角形?为什么?