题目内容
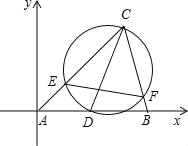
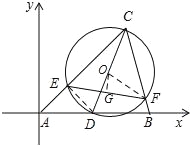
【题目】如图,在平面直角坐标系中,点A在坐标原点,∠CAB=45°,AC=2![]() ,∠ACB=60°,点B在x轴正半轴,点C在第一象限,动点D在边AB上运动,以CD为直径作⊙O与AC,AB分别交于E,F,连接EF.
,∠ACB=60°,点B在x轴正半轴,点C在第一象限,动点D在边AB上运动,以CD为直径作⊙O与AC,AB分别交于E,F,连接EF.
(1)当△CEF成为等边三角形时,AE:EC= ;
(2)当EF=![]() 时,点D的坐标为 .
时,点D的坐标为 .
【答案】1:![]() ;(
;(![]() ,0)
,0)
【解析】
试题分析:(1)连接ED可知,∠CED=90°,由∠CAB=45°,可得△AED是等腰直角三角形,又因为△CEF是等边三角形,所以∠CEF=60°,由圆周角定理可知∠ACD=30°,由锐角三角函数tan∠DCE=![]() ,所以
,所以![]() ;
;
(2)过点O作OG⊥EF于点G,由垂径定理可求得OF=![]() ,即可以求出直径CD=
,即可以求出直径CD=![]() ,然后设AE=x,利用勾股定理可得:ED2+CE2=CD2,即x2+(2
,然后设AE=x,利用勾股定理可得:ED2+CE2=CD2,即x2+(2![]() ﹣x)2=
﹣x)2=![]() ,即可求出DE的长度
,即可求出DE的长度![]() ,而AD=
,而AD=![]() AE=
AE=![]() ,即可得D的坐标为(D的坐标为(
,即可得D的坐标为(D的坐标为(![]() ,0).
,0).


练习册系列答案
 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案
相关题目